объем правильной призмы:
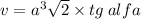
Объяснение:
1. ABCDA1B1C1D1 - правильная четырехугольная призма, => ABCD - основание призмы квадрат, боковые рёбра AA1, BB1, CC1, DD1 _|_ основаниям
диагональ квадрата AC = d=a√2, а - сторона основания призмы
2. рассмотрим прямоугольный треугольник:
катет AC =а√2 -диагональ квадрата
<С1АС = альфа - угол между диагональю призмы и плоскостью основания призмы
катет СС1 - боковое ребро - высота призмы
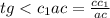
СС1=tg <C1AC × AC
CC1= a√2×tg альфа
V=a×а×c, где a, а, c - измерения правильной призмы
V = a× a × а√2× tg альфа
V = a^3 × √2 × tg альфа
Есть несколько решения этой задачи.
1) Есть точка на прямой А(3; 5; -2) и её направляющий вектор (-4; 3; -12) с модулем √(16+9+144) = 13.
Вектор АР = (-1; -3; 5). его модуль равен √(1+9+25) = √35.
Найдём угол между ними.
cos A = |-4*-1+3*-3+(-12)*5|/(13*√35) = 65/13√35 = 5/√35.
Найдём синус угла: sin A = √(1 - cos²A) = √(1 - (25/35)) = √(10/35)/
Теперь находим расстояние от точки Р до прямой, равное отрезку АР, умноженному на синус угла.
d = √35*(√(10/35) = √10.
2) Площадь параллелограмма лежащего на двух векторах M0M1 и s:
S = |M0M1 × s|
M0M1 × s =
i j k
1 3 -5
-4 3 -12
= i 3·(-12) - (-5)·3 - j 1·(-12) - (-5)·(-4) + k 1·3 - 3·(-4) =
= i -36 + 15 - j -12 - 20 + k 3 + 12 =
= -21; 32; 15.
Зная площадь параллелограмма и длину стороны найдем высоту (расстояние от точки до прямой):
d = |M0M1×s| |s| = √((-21)² + 32² + 15²) √((-4)² + 3² + (-12)²) =
= √1690 /√169 = √10 ≈ 3.1623.