Хотя бы озаглавили как-то-как называть углы
Договоримся-там,где 134 будет А,вершина В,потом С,а в центре D
Рассматриваем треугольник АВС
Внешний угол равен 134 градуса,значит смежный ему внутренний угол равен
180-134=46 градусов
И этот угол А поделён на две равные части(по условию задачи),
<ВАD=<DAC=46:2=23 градуса
Рассматриваем треугольник АDC,нам известны два угла,можем найти третий
<АСD=180-(23+108)=49 градусов
Рассмотрим треугольник АВD,по условию задачи он равнобедренный,т к АD=DB,из этого следует,что углы прикосновении равнобедренного треугольника равны между собой,т е
<ВАD=<ABD=23 градуса
Сумма всех углов треугольника 180 градусов
<АDB=180-23•2=134 градуса
Остался треугольник ВDC
Тут имеется внешний угол,равный 90 градусов,значит смежный ему внутренний угол С равен тоже 90 градусов,но он состоит из двух углов
<АСD=49 градусов,значит
<DCB=90-49=41 градус
Есть такое правило-два внутренних угла треугольника равны внешнему углу не смежного с ними
Внешний угол равен 134 градуса,значит
<В+<С=134 градуса,<С=90 градусов,значит <В=134-90=44 градуса
<АВD=23 градуса
СВD=44-23=21 градус
Треугольник ВDC поделён на 2 треугольника,обозначим отрезок,который из точки D опущен на сторону ВС,DE
В треугольнике ВDC мы знаем два угла,угол ВDC=180-(21+41)=118 градусов
По условию задачи известно,что
<BDE=<EDC=118:2=59 градусов
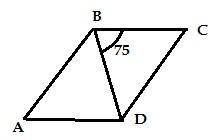
Объяснение:
сторона = 8 см
площадь = 40,74 см²
Объяснение:
1. BC -6 см, BD - 7 см. CD - ?
Вторую сторону параллелограмма CD находим по теореме косинусов:
CD² = BC² + BD² - 2 * BC * BD * Cos B
По таблице Брадиса примем значение косинуса 75° = 0,25
CD² = 36 + 49 - 2 * 6 * 7 * 0.25 = 64
CD = 8
2. Площадь треугольника ВСD - это 1/2 площади параллелограмма ABCD. Найдем S Δ ВСD через синуса угла B и умножим ее на 2.
S Δ ВСD = 1/2 * BC * BD * Sin 75, ⇒ S ABCD = BC * BD * Sin 75
Sin 75 по таблице Брадиса примем 0,97
S ABCD = 6 * 7 * 0.97 = 40.74 см²