150 см²
Объяснение:
Площадь прямоугольного треугольника равна половине произведения катетов.
Пусть гипотенуза с=5х см, тогда катет а=4х см, катет b=15 cм по условию.
По теореме Пифагора с²=а²+b²
(5х)²=(4х)²+15²
25х²-16х²=225
9х²=226
х²=25
х=5 и х=-5 (не подходит)
а=5*4=20 см
S=1/2 * 20 * 15 = 150 (см²)
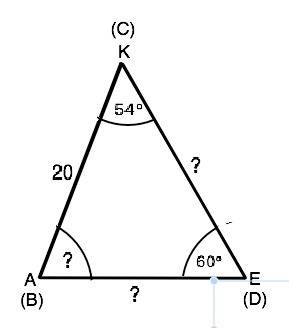
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см
Так как пирамида правильная четырехугольная, то основания - квадраты. Меньшее из них имеет сторону, равную 2 (по условию), и диагональ его равна "2 корня из 2". Большее основание имеет сторону 10 (по условию) и диагональ "10 корней из 2".
Вершины меньшего основания проецируются на диагонали большего. Величина отрезка, соединяющего вуершину большего основания с точкой, являющейся проекцией вершины меньшего основания на большее, равен ("10 корней из двух" - 2 корня из двух")/2 = "4 корня из 2".
Высота усеченной пирамиды равна 7 (по условию. Тогда квадрат бокового ребра будет равен (согласно теореме Пифагора) "4 корня из 2" + 7^2 = 32 + 49 = 81, , а боковое ребро корню из 81, т.е. 9.
ответ: 9
Пусть катет 4х см, а гипотенуза 5х см.
Тогда по теореме Пифагора гипотенуза равняется:
(4х)²+15²=(5х)²
16х²+225=25х²
25х²-16х²=225
9х²=225
х²=225/9
х²= 25
х1=5
х2=-5 (но такого не может быть в треугольнике)
катет второй: 5*4=20 см
Площадь прямоугольного треугольника:
катет1*катет2/2
S=1/2 15*20=15*10=150 см^2