1))). Если луч есть биссектриса угла, то любая точка его равноудалена от сторон этого угла.
2))). Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
3))). 1. Точка пересечения биссектрис треугольника- центр вписанной окружности ;
2. Точка пересечения серединных перпендикуляров треугольника- центр описанной окружности ;
3. Точка пересечения медиан треугольника (медианы треугольника пересекаются в отношении 2:1)
4. Точка пересечения высот треугольника - ортоцентр фигуры (центр вписанной и описанной окружности).
Объяснение:
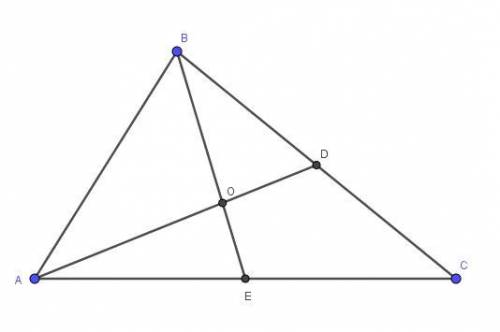
Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть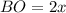 
см и 
см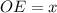, тогда 
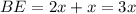, что по условию он равен 9 см.
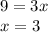
Следовательно,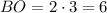 
см и 
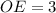см
Аналогично, пусть теперь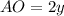 
см и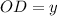 
, тогда 
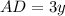и по условию равен 12 см
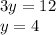
Таким образом,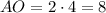 
см и 
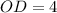см.
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника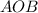 
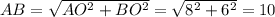см
По теореме Пифагора из прямоугольного треугольника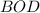 
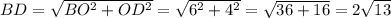см
Тогда 
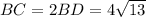см
Из прямоугольного треугольника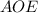 
по теореме Пифагора
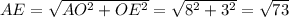см
Тогда 
см
ответ: 
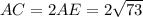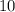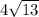см;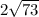 
см; 
см.
теперь 36 умножаем на один из элементов соотношения.
нам нужно узнать меньший угол =>
36*2=72