Объяснение:
1. вектор AB + вектор BD= вектор AC + вектор CD
2. вектор AB + вектор BC= вектор AD + вектор DC
Это правило треугольника сложения векторов: Видим что конец первого вектора совпадает с началом второго. Значит результатом сложения будет вектор, обозначенный первой буквой первого вектора и второй буквой другого вектора:
АВ + ВD = AD, AC + CD = AD
Видим, что результаты сложения совпадают, что и требовалось доказать.
Аналогично и во втором примере:
AB + BC = AC, AD + DC = АС, что и треб. доказать.
АВСD - параллелограмм
1. CA = СВ + ВА = CD + DA
2. DA = DC + CA = DB + BA
1. вектор AB + вектор BC = AC
2. вектор MN + вектор NN = MN
3. вектор PQ+ вектор QR = PR
4.вектор EF + вектор DE = DE + EF = DF
выразите вектор BC через векторы AB и AC:
BC = AC - AB
взята точка D на стороне треугольника ABC. Выразите вектор BD через векторы AB и AD:
BD = AD - AB
Дан параллелограмм ABCD. Найдите разность:
1. вектор AB- вектор AC = CB
2. вектор BC - вектор CD = AB+BC = AC
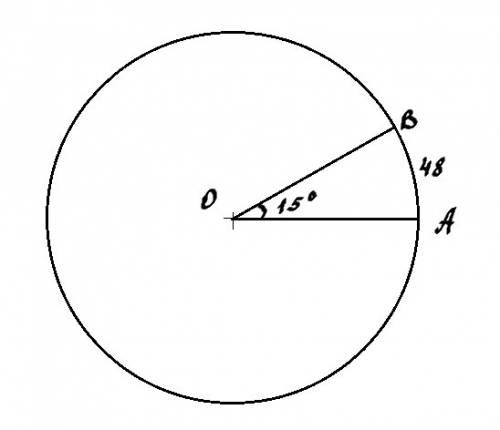
Угол АОВ центральный (смотри рисунок). Его градусная мера равна градусной мере дуги, на которую он опирается.
Малая дуга АВ равна 15°. Длина же ее равна 48.
Решим задачу, используя отношение.
Во сколько раз градусная мера большой дуги АВ больше градусной меры малой дуги АВ, во столько же раз длина большой дуги АВ больше длины малой дуги АВ.
Градусная мера всей окружности 360°.
360°–15° = 345° – градусная мера большой дуги АВ.
345°:15° = 23.
В 23 раза градусная мера большой дуги АВ больше градусной меры малой дуги АВ.
48*23 = 1104 – длина большой дуги АВ.
ответ: 1104.