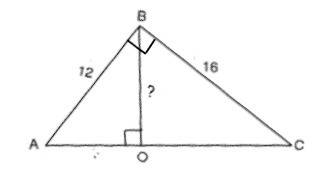
По т.Пифагора найдём гипотенузу.
АС=√(BC²+AC²)=√(256+144)=20 см
Высоту BO проще всего найти из площади треугольника.
S=BC•AB/2
S=BO•AC/2 Следовательно,
BC•AB=BO•AC, откуда
BO=BC•AB:AC
BO=16•12:20=9,6 см
-----
Вариант решения ( несколько длиннее) - его алгоритм дан ниже.
1) Находим гипотенузу по т.Пифагора
2) Катет прямоугольного треугольника – среднее пропорциональное между гипотенузой и проекцией этого катета на неё. ⇒
АВ²=АС•АО, ⇒ АО=АВ²:АС Отрезок СО находим вычитанием АО из гипотенузы или тем же что АО.
3) Высота прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу. ⇒
ВО²=СО•АО. Вычисления дадут ту же длину ВО=9,6 см
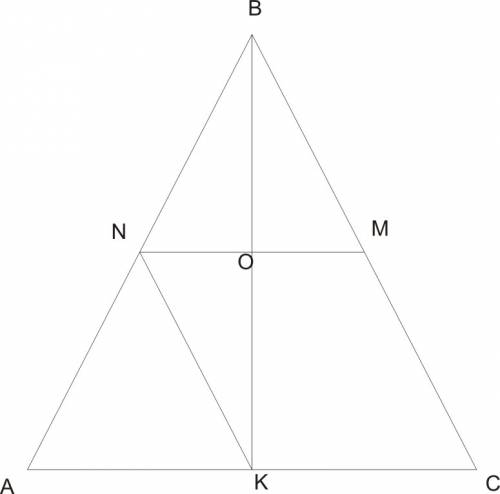
Δ АВС - равнобедренный
ВК = 30 см - биссектриса к основанию АС, она же и медиана Δ АВС ⇒ АК=КС
NM = 16 см - средняя линия II АС ⇒AN=NB
NK = ? - средняя линия II ВС
NM x ВК в т.О и деляться ей пополам, т.к. Δ NMB подобен Δ АВС по 3-м углам, ⇒ Δ NMB равнобедренный и ВО его высота, биссектриса и медиана.
ВО=ВК т.к. NM средняя линия Δ АВС
Получаем
NO=1/2NM= 16/2=8
OK=1/2ВК= 30/2=15
Δ NOK прямоугольный, т.к. уже доказано, что BO высота Δ NMB ⇒ <BON = 90°
<NOK - смежный и =180°-<BON = 90°
По теореме Пифагора находим NK - гипотенузу Δ NOK
NK=√(NO²+OK²) = √(8²+15²)=√(64+225)=√289=17 см
tg(∠ВСД)=ВД/СД=2СД/СД=2.
∠ВСД=arctg2≈63.4° (!).
Тр-ник АВС - прямоугольный, ∠АВС=90°, т.к. АВ и ВС - касательная и диаметр.
∠ВАС=90-∠ВСА=90-63.4≈26.6° (!).
(!) - это ответы.