Для того, чтобы найти величину третьего внешнего угла треугольника мы прежде всего должны вспомнить чему равна сумма всех внешних углов треугольника.
Но прежде всего давайте посмотрим, что нам дано в условии. Итак, нам известно, что два внешних угла треугольника равны 120° и 160°.
Сумма внешних углов треугольника равна 360°. Для того, чтобы найти чему равен третий внешний угол треугольника мы должны из 360° вычесть сумму двух других углов треугольника.
Давайте вычислим,
360° - (120° + 160°) = 360° - 280° = 80°.
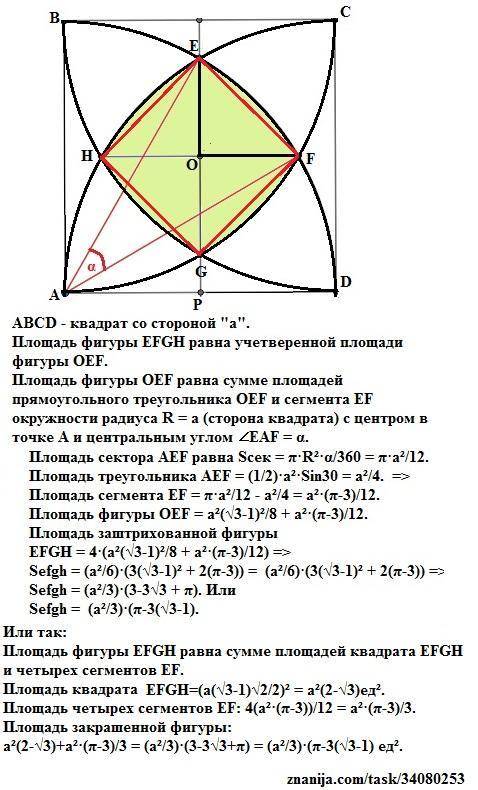
Sefgh = (a²/3)·(π-3(√3-1) ед².
Объяснение:
Пусть АВСD - квадрат со стороной "а".
Площадь фигуры EFGH равна учетверенной площади фигуры OEF.
Площадь фигуры OEF равна сумме площадей прямоугольного треугольника OEF и сегмента EF окружности радиуса R = a (сторона квадрата) с центром в точке А и центральным углом ∠EAF = α.
В треугольнике АЕР по Пифагору: ЕР = √(а²-а²/4) = а√3/2. =>
EO = EP-OP = а√3/2 - a/2 = а(√3-1)/2.
В треугольнике OЕF по Пифагору:
ЕF = √(OE² + OF²) = √(2·(a(√3-1)/2)²) = a(√3-1)√2/2.
Площадь треугольника OEF равна Soef = (1/2)·OE·OF = a²(√3-1)²/8.
По теореме косинусов в треугольнике AEF найдем угол EAF = α.
Cosα = (a² + a² - EF²)/2a² = (2a² - (a(√3-1)√2/2)²)/2a² = 2a²(4 - 3 +2√3 - 1)/(4·2a²) = √3/2.
α = arccos(√3/2) = 30°.
Найдем площадь сегмента EF, отсекаемого от круга (А;R) хордой EF по формуле:
S = Sc - Saef, где Sc - площадь сектора AEF, а Saef - площадь треугольника AEF.
Площадь сектора AEF равна Sсек = π·R²·α/360 = π·а²/12.
Площадь треугольника AEF = (1/2)·а²·Sin30 = а²/4. =>
Площадь сегмента EF = π·а²/12 - а²/4 = а²·(π-3)/12.
Площадь фигуры OEF = a²(√3-1)²/8 + а²·(π-3)/12.
Площадь заштрихованной фигуры
Sefgh = 4·(a²(√3-1)²/8 + а²·(π-3)/12) =>
Sefgh = (a²/6)·(3(√3-1)²+2(π-3))= (a²/6)·(3(√3-1)² + 2(π-3)). =>
Sefgh = (a²/3)·(3-3√3 + π).
Sefgh = (a²/3)·(π-3(√3-1) ед².
Или так:
Площадь фигуры EFGH равна сумме площадей квадрата EFGH и четырех сегментов EF.
Площадь квадрата EFGH= (a(√3-1)√2/2)² = a²(2-√3)ед².
Площадь четырех сегментов EF: 4(а²·(π-3))/12 = а²·(π-3)/3.
Площадь закрашенной фигуры:
a²(2-√3)+а²·(π-3)/3 = (a²/3)·(3-3√3+π) = (a²/3)·(π-3(√3-1) ед².