Боковое ребро наклонной призмы равно 14 см и составляет с плоскостью основания угол 30º. Нужно найти высоту призмы.
-------------
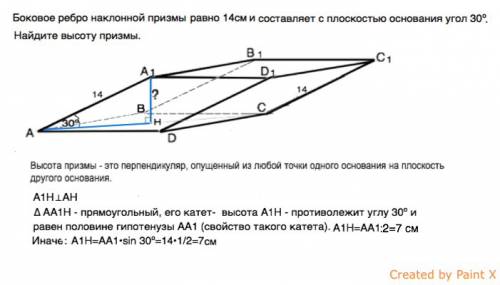
Высота призмы - это перпендикуляр, опущенный из любой точки одного основания на плоскость другого основания.
Т.к. основания лежат в параллельных плоскостях, высота призмы равна расстоянию между плоскостями, содержащими её основания.
Обозначим вершины призмы ABCDA1B1C1D1 (см.рисунок в приложении)
Опустим из вершины А1 перпендикуляр А1Н на плоскость основания.
А1Н ⊥АН
∆ АА1Н - прямоугольный, его катет- высота призмы А1Н - противолежит углу 30º и равен половине гипотенузы АА1.
А1Н=14:2=7 см
Иначе: А1Н=АА1•sin 30º=14•1/2=7см
–––––––––
Примечание:
Высота призмы не обязательно совпадает с высотой боковой грани. Она совпадает с ней, только если призма прямая. В данном случае призма - наклонная.
1)Квадрат диагонали в прямоугольном параллепипеде равен сумме квадратов измерений, тогда если диагональ обозначить через C, то составим уравнение?
С в квадрате = 25 + 49 + 47 = 121
С = 11
2)Найдем синус угла образованного диагональю с плоскостями оснований. По моему рисунку как будто у меня у параллепипеда высота равна 7. Если у тебя высота параллепипеда равна 5 либо корню из 47, поменяй в моем решении числа местами. в общем на чертеже тебе надо провести проекцию диагонали - угол между ней и самой диагональю - тот самый. Его синус равен высоте поделенной на диагональ (по теореме пифагора). Итак:
Синус угла = 7 / 11.
ответ: а) 11; б) 7/11.
Объяснение:
7-3=4