ответ:4)а 5)в 6)б 7)в
Объяснение:4)Т.к центральный угол О =100°=> и дуга, на которую он смотрит тоже равна 100°,тогда х=50,потому что он вписаный(вписаный угол равен половине дуги ,на которую он опирается)
5)угол равен 70,тогда дуга равна 140(описанный угол,дуга в 2р больше него)
Вся окружность =360
360-140=220(это дуга,на которую смотрит х),тогда сам х=220:2=110(угол вписанный)
6)О=64,дуга тоже 64(центральный),х описанный =64/2=32
7)Т.к ВО(это радиус)=АД,то АД=ДО т.к ДО тоже радиус,тогда ВО в 2р меньше ВО,угол В=90 т.к радиус ,проведенный в точку касания явл. перпендикуляром на эту касательную.Тогда мы можем применить свойство треугольника :сторона,лежащая напротив угла в 30°=половине гипотенузы ,тогда угол ВАО=30,а ВАО=ОВС т.к это касательные вышли из 1ой точки,тогда угол ВАС=60
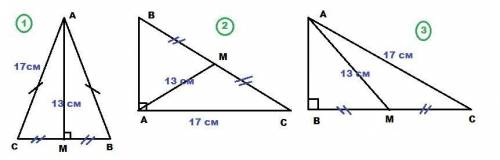
Задача с неполным условием, имеет бесконечно много решений в зависимости от вида треугольника. Рассмотрим три возможных варианта.
1) ΔABC - равнобедренный, AC = AB; AM=13 см; AC = 17 см
AM - медиана, в равнобедренном треугольнике одновременно высота ⇒ CM = MB; AM⊥CB
ΔAMC - прямоугольный, ∠AMC=90°; AM=13 см; AC = 17 см
Теорема Пифагора :
CM² = AC² - AM² = 17² - 13² = 120 = (2√30)²
CM = 2√30 см
BC = 2 CM = 2 · 2√30 = 4√30 см
BC = 4√30 см
=========================================
2) ΔABC - прямоугольный; ∠BAC = 90°; AM=13 см; AC = 17 см
AM - медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
BC = 2 AM = 2 · 13 = 26 см;
BC = 26 см
====================================
3) ΔABC - прямоугольный, ∠ABC = 90°; AM=13 см; AC = 17 см
AM - медиана ⇒ BM = MC; BC = 2BM
Теорема Пифагора
AB² = AC² - BC² = 17² - (2BM)² = 289 - 4BM²
Теорема Пифагора для ΔABM
AB² = AM² - BM² = 13² - BM² = 169 - BM²
169 - BM² = 280 - 4BM²
3BM² = 111; BM² = 37
BM = √37 см ⇒ BC = 2BM = 2√37 см
BC = 2√37 см
2 признак если два угла и сторона между ними соответственно равны 2 углам и стороне другого треугольника
3 признак если все стороны одного треугольника равны сторонам другого треугольника