если нижнее основание а, верхнее b, и искомый отрезок - длины х, то прощади трапеций будут такие
S1 = (b + x)*h1/2; S2 = (a + x)*h2/2;
или, поскольку S1 = S2,
(b + x)/(a + x) = h2/h1;
Чтобы получить соотношение между h1 и h2, проведем прямую, параллельную боковой стороне через конец отрезка х, лежащий на ДРУГОЙ боковой стороне.
Малое основание продолжим до пересечения с этой прямой. Получилось 2 подобных треугольника с основаниями (x - b) и (a - x); из подобия следует
h2/h1 = (a - x)/(x - b);
поскольку соответствующие высоты так же пропорциональны, как и стороны.
Итак, имеем уравнение для х
(b + x)/(a + x) = (a - x)/(x - b);
x^2 - b^2 = a^2 - b^2;
x = корень((a^2 + b^2)/2);
Подставляем численные значения, получаем
х = корень(24^2 + 7^2) = 25;
Надо же, и тут Пифагорова тройка (7,24,25)
1)
Площадь любого треугольника равна половине произведения высоты на сторону, к которой она проведена.
Формула высоты равностороннего треугольника равна
h=(а√3):2
а=1 м по условию задачи.
S=(1*1√3):2=0,5√3 м²
2)
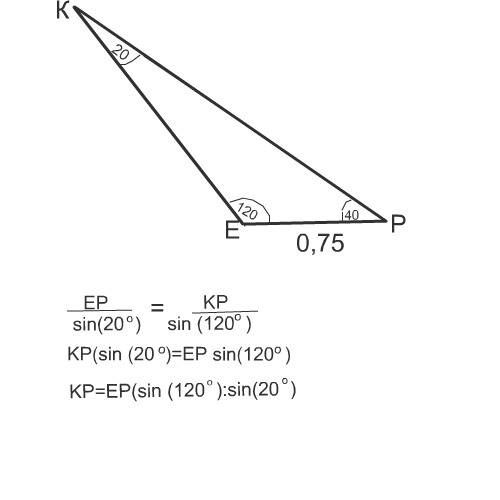
Для решения задачи следует применить теорему синусов. Ход решение дан во вложении, значения синусов найдете по таблице и без труда сделаете вычисления самостоятельно.
3)
Для решения задачи следует применить теорему косинусов:
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Cos(100°) -0.1736
Третья сторона равна корню квадратному из
(1806,25+1,69- 2·55,25· (-0.1736)=42,745 см²