1.
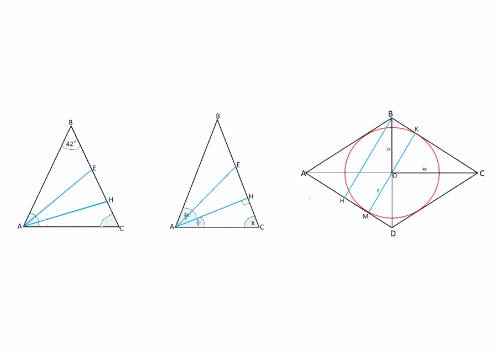
Треугольник АВС - равнобедренный.
Углы при основании АС равны.
Угол В=42°
Угол А=С=(180-42):2=69°
Угол А разделен на 3 равных угла.
Угол АНЕ=2/3 ВАС=69°:3·2=26°
------------------------------------
2.
Треугольник АВС - равнобедренный.
Угол А разделен на 3 равных угла.
Угол А=угол С=х
угол НАС=х:3
угол АНС=90° ( по условию)
Угол х+х:3=90°
3х:3+х:3=90°
4х=270°
х= 67,5
угол ВАН =67,6:3·2=45
Угол ВНА=90° ( по условию)
Угол АВН+угол ВАН=90°
угол АВН=90°- 45°=45°
------------------------------
3.
Радиус вписанной в ромб окружности равен половине диаметра.
Диаметр равен высоте ромба, т.к. перпендикулярен ВС и AD.
Высоту найдем из площади ромба.
Площадь ромба найдем через его диагонали по формуле:
S=d·D:2
Диагонали найдем из четвертой части ромба - Δ АОВ.
АОВ - прямоугольный треугольник с гипотенузой 25 и отношением катетов 3:4, т.к. диагонли относятся 3:4, отношений их половин также3:4
Длина катетов при этом отношении из египетского треугольника с отношением сторон 3:4:5
1часть этого отношения =25:5=5
ВО=3·5=15
ОС=4·5=20
(Можно проверить по т.Пифагора)
d=ВD=ВО·2=30
D=АС=ОС·2=40
S АBCD=d·D:2=600
По другой формуле площадь ромба
S ABCD=AD·BH
BH=S:AD
Высота ВН=600:25=24
Диаметр КМ=ВН=24
r=24:2=12
Радиус шара 15 см.
Вне шара дана точка А на расстоянии 10 см от его поверхности.
Найти
длину такой окружности на поверхности шара, все точки которой отстают от А на 20 см
Расстояние измеряется перпендикуляром. А находится на отрезке прямой, перпендикулярной диаметру искомой окружности.
Точка А от центра шара удалена на 15+10=25 см ( радиус + расстояние)
Все точки искомой окружности находятся на поверхности окружности основания воображаемого конуса, "надетого" на шар.
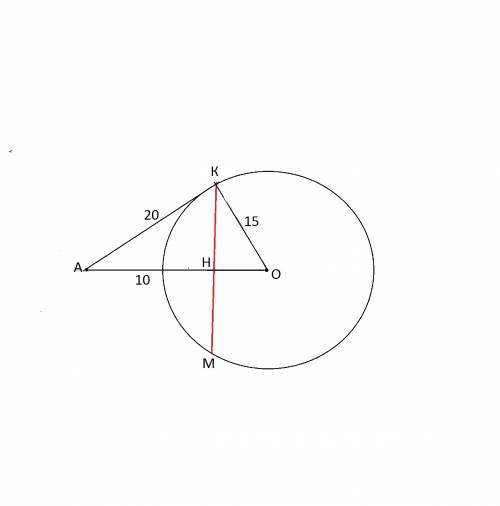
Смотрим схематический рисунок - разрез шара через центр и точку А.
АО=15+10=25 см.
ОК=R
АК - расстояние, на которое должна быть удалена точка А от поверхности.
КМ- диаметр искомой окружности,
КН - ее радиус.
Имеем треугольник АКО со сторонами, отношение которых 3:4:5 - отношение прямоугольного "египетского" треугольника.
Радиус искомой окружности КН - высота этого треугольика.
Чтобы найти высоту, применим свойство катета прямоугольного треугольника:
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.
Пусть отрезок гипотенузы, заключенный между катетом и высотой,
ОН =х
Тогда
ОК ²=х*25
25х=225
х=9
Из треугольника КНО
КН²=КО²-ОН²= 225-81=144
КН=r=12 см
Длина окружности с радиусом 12 см
С=2πr= 2π12=24π cм
(углы ркт равен углу ртк)
отрезок км равен мр и равны они высоте так как они катеты равнобедренного треугольника т высота в прямоугольной трапеции равно стороне км
треугольник крт равнобедренный а значит высота рс явл и биссектрисой а значит делит прямой угол крт пополам на углы по 45°, угол рст 90° так как рс высота а значит угол РТС равен 45° и значит треугольник рст равнобедренный и катеты рс и ст равны между собой и равны 6
кс равен мр так как явл сторонами квадраты которые равны 6
ответ на б: основания равны 6 и 12