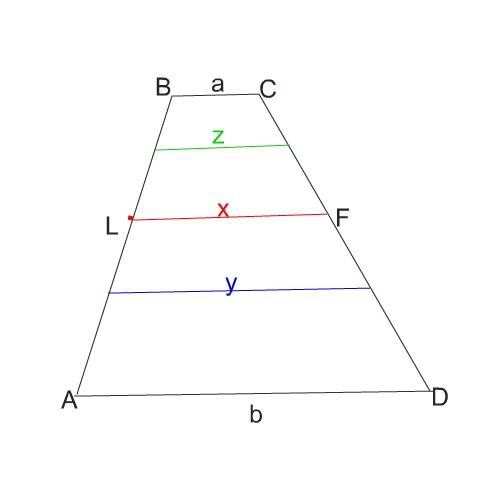
Обязательно смотрим рисунок.
И примем во внимание, что получающиеся трапеции подобны не исходной.
Если трапеции ALFD и LBCF подобны, то a/LF = LF/b.
Отсюда LF = √(ab).
Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований.
---
Делим трапецию:
1 отрезок между основаниями исходной:
х²=2*8=16
х=√16=4
Второй отрезок между первым и основанием исходной трапеции
у²=4*8=32
у =√32=4√2
Третий отрезок - идет под меньшим основанием
z²=2*4=8
z=2√2
---------------------------
Отрезки в рисунке идут в таком порядке
z, x, y
---------------
Коэффициент подобия между этими четырьмя трапециями попарно ( смежными) равен
4:2√2=2:√2=2√2:√2·√2=2√2:2=√2
k=√2
Площади подобных фигур относяся как квадрат коэффициента их подобия.
Для этих трапеций это
(√2)²=2
Площадь второй по величине относится к нижней -большей- как 1:2=1/2
Третьей ко второй 1/2:2=1/4
и последней
1/8
сложим площади
1/2+1/4+1/8 =( 4+2+1)/8=7/8
7/8 < 1
Площадь самой большой из этих четырёх трапеций больше суммы площадей остальных трёх
Здравствуйте
Задача решается простым уравнением.
Пусть длина боковой стороны равняется x, тогда длина основания x+7.
Теперь, легко составить уравнение. Периметр треугольника равен сумме его сторон.
2x+(x+7)=73
2x+x+7=73
3x=73-7
3x=66
x=22
Мы нашли длину боковой стороны - 22 см. И не одной, а сразу двух, так как в равнобедренном треугольнике они равны. Теперь мы можем узнать длину основания, подставив результат в выражение x+7
x+7=22+7=29 см
ответ: Длина боковой стороны - 22 см, длина основания - 29 см.
Рад, что смог
По теореме косинусов:
ответ: 2 ед.