Объяснение:
Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
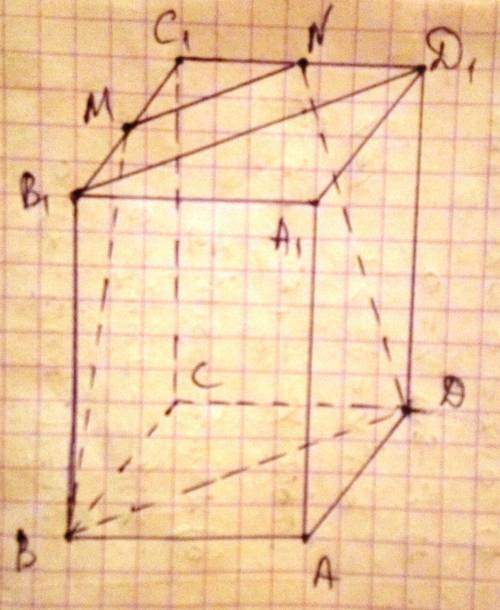
Пусть плоскость проведённая через B, D и серединную точку M ребра B₁C₁ пересекается с плоскостью B₁C₁А₁ по прямой MN. M∈B₁C₁, N∈D₁C₁.
⇒MN||BD⇒BDNM-трапеция
BD||B₁D₁; MN||BD⇒MN||B₁D₁
MN-средняя линия треугольника B₁C₁D₁
ABCDA1B1C1D1- правильный прямоугольный параллелепипед⇒ABCD-квадрат, а боковые грани прямоугольники.
B₁M=0,5B₁C₁=ND₁, DD₁=BB₁, ∠MB₁B=∠ND₁D=90°⇒ΔMB₁B=ΔND₁D⇒MB=ND⇒
⇒BDNM-равнобедренная трапеция. Ч.Т.Д.
достроим прямоугольник до квадрата со стороной a + b, как показано на рисунке 1.
так как площадь квадрата равна квадрату его стороны, то площадь этого квадрата равна (a + b)2.с другой стороны, этот квадрат составлен из данного прямоугольника с площадью s, равного ему прямоугольника с площадью s (так как, по свойству площадей, равные многоугольники имеют равные площади) и двух квадратов с площадями a2 и b2. так как четырехугольник составлен из нескольких четырехугольников, то, по свойству площадей, его площадь равна сумме площадей этих четырехугольников: (a + b)2 = s + s + a2 + b2, или a2 + 2ab + b2 = 2s + a2 + b2.отсюда получаем: s = ab, что и требовалось доказать.