Углы, образованные при пересечении двух параллельных прямых секущей, или равны, или в сумме составляют 180°. Следовательно, нам дано значение одного из смежных углов.
а) второй угол равен 180° - 150° =30°.
б) один из углов равен Х градусов, второй - Х+70 градусов. Их сумма равна 2Х+70=180° => X=55°. Тогда меньший угол = 55°, второй = 125°.
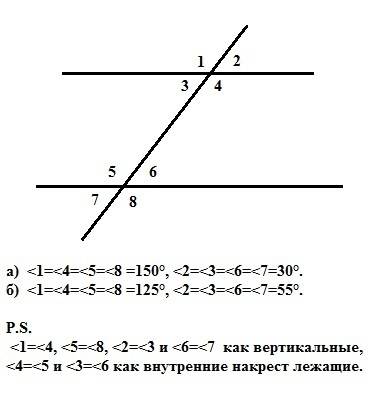
Или (см. рисунок): а) <1=<4=<5=<8 =150°, <2=<3=<6=<7=30°.
б) <1=<4=<5=<8 =125°, <2=<3=<6=<7=55°.
P.S.
<1=<4, <5=<8, <2=<3 и <6=<7 как вертикальные,
<4=<5 и <3=<6 как внутренние накрест лежащие.
Пусть ABCD - параллелограмм, угол A- острый. Из вершины B - опустим высоту BK и из вершины С высоту CM, тогда из треугольника ACM получим
AM^2=AC^2-CM^2=900-576=324
откуда AM=18
Из треугольника BDK имеем
KD^2=BD^2-BK^2=676-576=100
откуда KD=10
Так как AK=DM, то 2DM+KD=AM
откуда DM=(AM-KD)/2=(18-10)/2=4
Из треугольника CDM, имеем
CD^2=CM^2+DM^2=576+16=592
CD=4*SQRT(37)
BC=KM=KD+DM=10+4=14
AB=CD=4*SQRT(37)
BC=AD=14