72°; 54°; 54°.
Объяснение:
Дано:
Равнобедренный треугольник МРК.
АВ ║МР, точка А ∈ МК, точка В ∈ КР.
∠К = 72°, ∠ М = 54°
Найти: углы треугольника АВК.
Решение.
1. Так как Δ МРК является равнобедренным, то его углы при основании равны:
∠Р = ∠М = 54°.
2. Так как АВ ║ МР, то Δ ABK подобен Δ МРК, в силу чего:
∠АКВ треугольника АВК равен ∠К треугольника МРК:
∠АКВ = ∠К = 72°;
∠КАВ треугольника АВК равен ∠М треугольника МРК:
∠КАВ = ∠М = 54°;
∠КВА треугольника АВК равен ∠Р треугольника МРК:
∠КВА = ∠Р = 54°.
ответ: углы треугольника АВК равны 72° (угол при вершине), 54° и 54° (углы при основании).
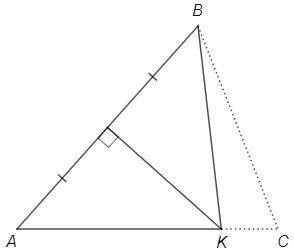
Точка K на серединном перпендикуляре к AB, следовательно равноудалена от концов отрезка, AK=BK.
Тогда по условию BK=BC+CK.
В треугольнике BCK сумма двух сторон равна третьей стороне - треугольник вырожденный, точки B-C-K лежат на одной прямой.
(Или можно сказать, что расстояние между конечными точками ломаной B-C-K равно длине ломаной => ломаная вырожденная, точки B-C-K на одной прямой.)
По условию точка K лежит на отрезке AC. Несовпадающие прямые AC и BC могут иметь только одну общую точку, следовательно точки K и С совпадают.
Тогда вершина С лежит на серединном перпендикуляре к основанию AB, AC=BC, △ABC - равнобедренный.
∠ 1=∠ 3 как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей АС.
Значит ∠ 2=∠3 и треугольник ACD - равнобедренный AD=CD=7 cм.
Трапеция ABCD - равнобедренная AB=CD=7 cм
ответ Р (трапеции)=7+7+7+3=24 см.