они действительно равны
Объяснение:
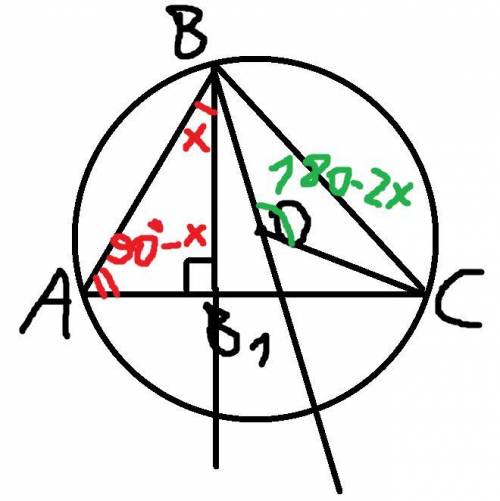
Пусть <ABB1 = x, тогда если <BB1A = 90 градусов (т.к. BB1 - высота), то ABB1 = (180 - 90 - x) градусов = (90 - x) градусов. Т.к. <BAC - вписанный для дуги BC, а <BOC - центральный для этой же дуги BC, то <BOC = 2*<BAC = 2*(90 - x)градусов = (180 - 2x) градусов. Очевидно, что BO = OC = R, тогда треугольник BOC - равнобедренный, тогда <CBO = <BCO = (180 - < BOC) / 2 = (180 - (180 - 2x)) / 2 = 2x / 2 = x. Следовательно <ABB1 = <CBO = x.
пусть один угол равен Х, тогда второй равен 3/10Х, а третий равен 3/10Х+20.
Составим уравнение.
Х+3/10Х+3/10Х+20=180
Х+6/10Х=160
Х+3/5Х=160
8/5Х=160
Х=160:8/5
Х=160*5/8
Х=100
100 градусов - один угол
100* 3/10= 30 градусов - второй угол.
30+20= 50 градусов - третий угол.
Проверка: 100+30+50=180 градусов - сумма углов треугольника.