 с прямым углом
с прямым углом  , EF — биссектриса
, EF — биссектриса  ,
,  , FG — искомый отрезок.
, FG — искомый отрезок.  .
.  — биссектриса, то
— биссектриса, то  (биссектриса
(биссектриса  делит
делит  на два равные угла).
на два равные угла). 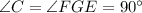 (это следует из условия: так как
(это следует из условия: так как  прямоугольный, то и
прямоугольный, то и  ; так как
; так как  — расстояние от
— расстояние от  до
до 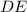 , то
, то 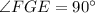 ).
).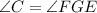 и
и 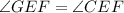 , то и третий угол первого треугольника равен третьему углу второго треугольника:
, то и третий угол первого треугольника равен третьему углу второго треугольника:  . Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так:
. Это следует из того факта, что сумма углов любого треугольника равна 180°. Тогда можно записать так: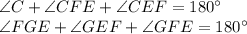
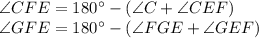
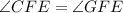 .
.  является для обоих треугольников общей.
является для обоих треугольников общей. (второй признак равенства треугольников — по стороне и двум прилежащим к ней углам (
(второй признак равенства треугольников — по стороне и двум прилежащим к ней углам ( — сторона, а
— сторона, а  — два прилежащих угла)).
— два прилежащих угла)). соответствует
соответствует  , тогда:
, тогда: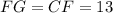
 . Смотрите второй рисунок.
. Смотрите второй рисунок.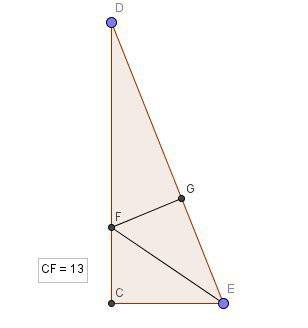
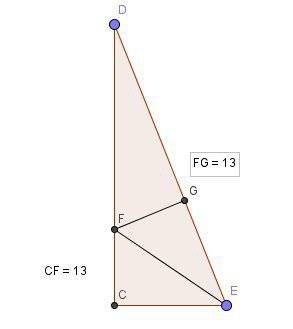
Например, для ∠A∠A, внешними будут углы ∠1∠1 и ∠2∠2 (см. рис.)

Свойства внешних углов треугольника
Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна 360∘360∘.
Сумма внешнего и внутреннего угла при одной вершине равна 180∘180∘.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
∠1=∠B+∠C∠1=∠B+∠C
Примеры решения задач
Задание. В треугольнике ΔMNKΔMNK, внешний угол ∠M∠M равен 120∘120∘, а угол ∠N=65∘∠N=65∘. Найти угол ∠K∠K.
Решение. По теореме о внешнем угле∠M=∠N+∠K∠M=∠N+∠K. Подставляя в это равенство исходные данные, получим
120∘=65∘+∠K120∘=65∘+∠K
Выразим ∠K:∠K=120∘−65∘⇒∠K=55∘∠K:∠K=120∘−65∘⇒∠K=55∘
ответ. ∠K=55∘∠K=55∘
Задание. Внешние углы при двух вершинах треугольник равны 70∘70∘ и 150∘150∘. Найти внутренний угол при третьей вершине.
Решение. Обозначим внешние углы ∠1,∠2,∠3∠1,∠2,∠3, а соответствующие им внутренние -