Если из внешней точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.
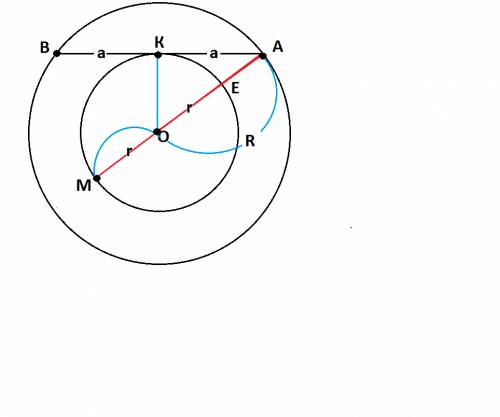
Для меньшей окружности точка А на большей окружности является внешней точкой.
АК²=АЕ*АМ
АЕ=R-r
AM=R+r
Пусть АК=а.
Тогда а²=(R-r)(R+r)=(R² -r²)
Т=π(R² -r²)⇒
Т=π*а²⇒
а=√(Т/π)
АВ=1а=2√(Т/π)
d^2=a^2+b^2+c^2;
36=x^2+4x^2+4x^2=9x^2;
x^2=36:9=4;
x=2.
AD=2 см, DC=4 см, DD1=4 см.
S бок.=P осн.*h=2*(2+4)*4=48 кв.см.
ответ: 48 кв.см.