ответ:√137 (ед. длины)
Объяснение:
Площадь треугольника равна половине произведения высоты на сторону, к которой проведена. Тогда: Ѕ=а•h:2 ⇒ a•h=2S
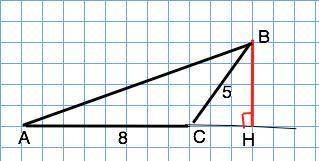
Высота тупоугольного треугольника, проведенная из вершины острого угла, проходит вне треугольника и пересекает продолжение стороны, к которой проведена.
В ∆ АВС проведенная к стороне, равной 8 см, высота ВН=2•16:8=4. Тогда в "египетском" треугольнике ВСН отрезок СН=3 ( то же получим по т.Пифагора).
Треугольник АВН - прямоугольный, АН=8+3=11. По т.Пифагора его третья сторона АВ=√(АН²+BH²)=√(11²+4²)=√137
Дано :
Четырёхугольник ABCD — параллелограмм.
S(ABCD) = 36 см².
Точка О — точка пересечения диагоналей АС и BD.
ОН — расстояние от точки О до CD, OH = 3 см.
ОМ — расстояние от точки О до AD, AD = 2 см.
Найти :
Р(ABCD) = ?
Расстояние от точки пересечения диагоналей параллелограмма до стороны в два раза меньше соответствующий высоте (высоте, которая проведена к этой же стороне).
Следовательно —
Высота МF = 2*OM = 2*2 см = 4 см
Высота ЕН = 2*ОН = 2*3 см = 6 см.
Площадь параллелограмма равна произведению стороны и высоты, опущенной на эту сторону.
Отсюда —
S(ABCD) = MF*AD
36 см² = 4 см*AD
AD = 36 см²/4 см = 9 см
S(ABCD) = ЕН*CD
36 см² = 6 см*CD
CD = 36 см²/6 см = 6 см.
Периметр параллелограмма равен удвоенной сумме двух его смежных сторон.
Следовательно —
P(ABCD) = 2*(CD + AD) = 2*(6 см + 9 см) = 2*15 см = 30 см.
30 см.
ответ: 48 градусов.