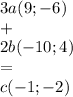
Пусть точка вне плоскости М.
Т.к. она равноудалена от вершин треугольника АВС, то ее перпендикуляр МН (расстояние до треугольника) опускается в центр описанной около треугольника окружности. Центр описанной около прямоугольного треугольника окружности лежит в середине гипотенузы.
Значит НВ = АВ:2 = 6см
Получился прямоугольный треугольник МВН: гипотенуза МВ = 10см,
катет НВ = 6см и катет МН, который нужно найти.
Теорема Пифагора
МН² = МВ² - НВ² = 100 - 36 = 64 = 8²
ответ: расстояние от точки до плоскости 8 см
Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
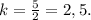
Отсюда -
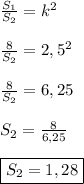
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
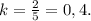
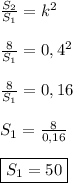
50 (ед²).