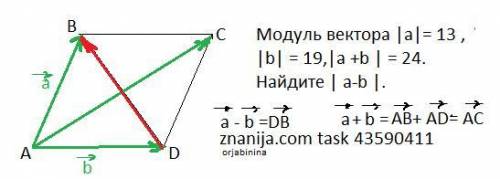
Модуль вектора |a|= 13 ,|b| = 19,|a +b | = 24. Найдите | a-b |.
Объяснение:
1) Рассмотрим ΔАВС, вектор а лежит на стороне АВ, вектор b лежит на стороне АD . Разность векторов а-b=DВ ( вектор) Уточняю длина ( или модуль) вектора равна длине отрезка на котором он лежит. Значит нужно найти отрезок DВ и АВ=13,АD=19 .
2) Достроим ΔАВD до параллелограмма , тогда сумма векторов а+b=АВ+АD=( по правилу параллелограмма ) = вектору АС. Тогда |AC|=|a+b|=24. Значит длина отрезка АС=24. По свойству диагоналей параллелограмма АО=12( О-точка пересечения диагоналей).
3) По свойству диагоналей параллелограмма: "сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон " имеем: AC²+BD²=2(AB²+AD²)
24²+BD²=2(13²+19²), BD=√(2*(169+361)-576)=√484=22.
Т.к. АС гипотенуза, становится ясно, что высота проведена из прямогу угла. А у такой высоты есть свойство, она равна среднему геометрическому отрезков нв которые она делит сторону к которой проведена. Т.е. в нашем случае АС^2=AD^2*DC^2. Найдем отсюда АC. DА=корень из(24^2-18^2)=корень из(252)
Теперь для начала найдем cosA. cosA=sinC(cвойство для прямоугольного треугольника)
а sinC в свою очередь равен24/BC. BC най дем по теореме пифагора из треугольника BDC. BC= корень из (24^2+18^2)=30 cosA=0,8
найдем АВ. Найдем по теореме Пифагора из треуг АВD. АВ=корень из(24^2+252)=
корень из(828)
AB=AD
Во 2-ых угол ВАС = DAC
в 3)сторона АС -общая
Значит треугольник ABC =треугольнику ADC по двум (2) сторонам и углу между ними (что и требовалось доказать )