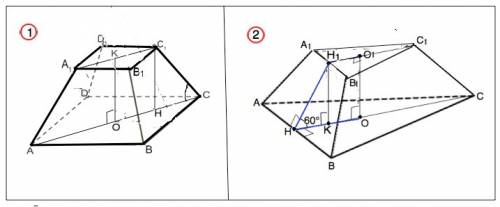
1)
Пирамида правильная, диагональное сечение - равнобедренная трапеция АА1С1С с основаниями АС=9√2 и А1С1=3√2
Высота С1Н=СН•tg60°
CН=(АС-А1С1):2=3√2=>
C1H=3√2√2=6
S(AA1C1C)=(AC+A1C1)•CH:2=(9√2+3√2)•6:2=36√2 (ед. площади).
2)
Боковые грани правильной усеченной пирамиды - равнобедренные трапеции.
S (бок) равна сумме их площадей.
Для решения задачи необходимо найти стороны оснований и их высоту.
Формула площади правильного треугольника
S=(a²√3):4=>
a²=4S:√3
AB²=4•36√3:√3=144 => AB=√144=12
А1В1²=4•9√3:√3=36 => A1B1=√36=6
Основания правильной усеченной пирамиды параллельны, поэтому подобны.
k=A1B1:AB=12:6=1/2
Проведем в ∆ АВС высоту СН, в боковой грани АА1ВВ1 высоту НН1.
СН⊥АВ и АН=ВН
НН1⊥АВ и АН=ВН
Двугранный угол равен линейному углу между лучами, проведенными в гранях двугранного из одной точки его ребра перпендикулярно к нему.=>
Угол Н1НС=60°.
Точка О - центр правильного ∆ АВС ( в ней пересекаются его медианы) . Поэтому СО:ОН=2:1, ОН=СН:3
СН=ВС•sinCBH=12¨√3/2=6√3.
ОН=2√3
В трапеции НН1С1С опустим высоту Н1К.
ОК=О1Н1=ОН:2=√3
КН=ОН-ОК=√3
Из прямоугольного ∆ НН1К гипотенуза НН1=НК:cos60°=(√3):√3/2=2
S(AA1B1B)=(AB+A1B1)•HH1:2=18
S(бок)=3•18=54 (ед. площади)
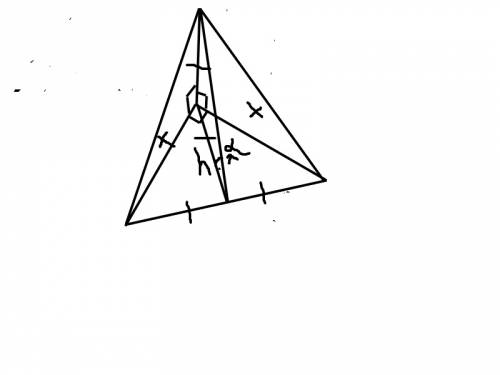
а)зная гипотенузу найдем катеты..по теореме пифагора: a²+b² = c² (a = b = х)
2х² = 32, х = √16 = 4.
теперь найдем высоту основания:
h ² = 16 - 8 = √8
так как угол α = 45 , то h основания = h пирамиды = ребро = √8. 1-е ребро
2-е и 3 -е найдем так же по теореме пифагора:
l = √16+8 = √24
б) S бок = S1 + S2 + S3
S1 = √8 * 4 /2 = 2√8 = 4√2 (S грани, прямоуголный треугольник)
S2 = √8 * 4 /2 = 2√8 = 4√2 (S грани, прямоуголный треугольник)
S3 = 4 * 4√2/2 = 8√2 (S грани, равнобедренный треугольник)
S = 16√2