1)угол ВМС = 180 - угол АМВ = 180-135 = 45 градусов (как смежные углы)
2)рассмотрим ΔВМС
угол СВМ = 180°-∠МСВ-∠ВМС = 180°-90°-45°=45°
⇒ ΔВМС - равнобедренный и прямоугольный
МС=СВ=10 см
3) сторона АС = АМ+МС = 6+10=16 СМ
4) ΔАВС - ПРЯМОУГОЛЬНЫЙ
Найдем АВ по теореме Пифагора
АВ- гипотенуза
АВ=√10²+16²=√100+256=√356 =2√89
5) Периметр ΔАВС = 2√89+16+10=2√89+26 = 2(√89+13)
Найдем полупериметр для дальнейшего нахождения площади по формуле Герона: (2(√89+13))/2=√89+13
6)Площадь:
√(√89+13)(√89+13-10)(√89+13-16)(√89+13-2√89) =
= √(√89+13)(√89+3)(√89-3)(13-√89) =
= √(13+√89)(13-√89)(89-9) = √(169-89)*80 = √80*80 = 80 см²
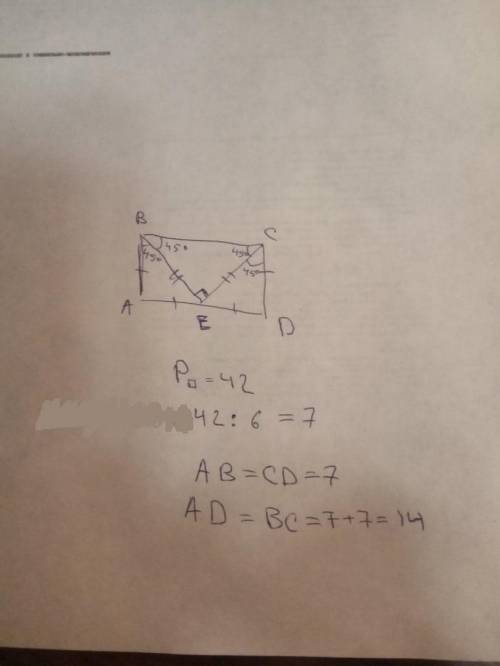
ответ: АВ=CD=7 AD=BC=14
Объяснение: назовем точку снизу как Е. треугольник ВЕС будет равнобедренным и прямоугольным, т.к. точка Е делит сторону АD пополам. Следовательно катеты треугольника будут равны и углы EBC и ECB будут равны 45 градусам. Далее следует что углы АВЕ, ECD, ВЕА и CED будут равны 45 градусам, и отсюда следует, что треугольники ABE и ECD так же равнобедренные и прямоугольные. Отсюда следует, что AB=AE=ED=CD, а сторона ВС = AD и BC = АЕ+ЕD.
Далее делим 42 на 6 = 7 (стороны АВ и CD)
а стороны AD и BC будут равны 7+7 = 14 , так как АЕ=ЕD
33sinx+12(sin²x+cos²x)=11
|sin²x+cos²x=1
=> 33sinx+12=11
33sinx=-1
sinx=-1/33
1)x=arcsin(-1/33)+2πn=-arcsin(1/33)+2πn,n∈Z
2)x=-π+arcsin(1/33)+2πn,n∈Z.