1)
Рассмотрим рисунок этой поделенной на 3 части трапеции.
Поведя из вершины у меньшего основания прямую, параллельную одной из боковых сторон, получили треугольник и параллелограмм.
Каждая из этих фигур разделена на 3 части.
В параллелограмме стороны равны, а части искомых отрезков равны меньшему основанию трапеции.
Треугольник же делится на подобные треугольники по свойству равенства углов при параллелльных прямых ( которые мы провели при разделении трапеции) и секущей, а угол при вершине этих треугольников - общий.
Так как боковая сторона разделена на 3 равные части, то отношение сторон этих треугольников 1:2:3
Основание большего треугольника (его боковая сторона=боковая сторона трапеции) равно разности оснований:
5 - 2=3
Т.к. боковая сторона трапеции разделена на 3 равные части, отношение сторон меньшего ( верхнего) треугольника и большего равно 1:3
Следовательно, его основание равно
⅓ ·3=1 см
Отношение второго по величине треугольника и большего равно
2:3, отсюда его основание равно
⅖·3=2 см
Так как длина каждого из проведенных параллелльных отрезков больше оснований треугольников на 2, то:
длина искомых отрезков равна:
1 см+2=3 см
2см+2=4см
--------------------------------
2)
Стороны треугольника MNP относятся к сторонам АВС как 1:3,т.к. каждая сторона Δ АВС разделена в отношении 1:2. И эта одна часть - сторона Δ MNP, стороне же АВС остаются её 3 части.
Треугольники АВС и MNP подобны, так как их сходственные стороны пропорциональны и коэффициент подобия этих треугольников
k=1/3
Площади подобных фигур относятся, как квадрат их коэффициента подобия, а в этой задаче в отношении (1/3)²=1/9.
Площадь Δ MNP=1/9 площади тр-ка АВС и равна 1/9 от S или S/9
----------------
3)
Площади подобных фигур относятся, как квадрат их коэффициента подобия. Т.к. площади квадратов относятся как 25:9, то коэффициент подобия ( отношение сторон квадратов) равен
k=√(25/9)=5/3
Пусть сторона меньшего квадрата равна х.
Тогда сторона большего равна х+10
(х+10):х=5:3
По свойству пропорции
3(х+10)=5х
3х+30=5х
2х=30
х=15
Сторона меньшего квадрата равна 15
Проверка:
Площадь большего квадрата
(15+10)²=625
площадь меньшего
15²=225
625:225=25:9
1)
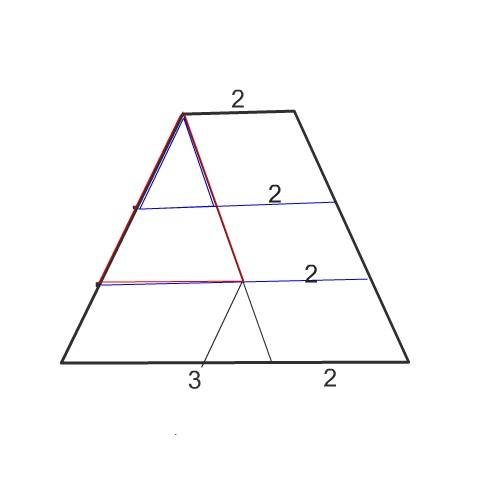
Рассмотрим рисунок этой поделенной на 3 части трапеции.
Поведя из вершины у меньшего основания прямую, параллельную одной из боковых сторон, получили треугольник и параллелограмм.
Каждая из этих фигур разделена на 3 части.
В параллелограмме стороны равны, а части искомых отрезков равны меньшему основанию трапеции.
Треугольник же делится на подобные треугольники по свойству равенства углов при параллелльных прямых ( которые мы провели при разделении трапеции) и секущей, а угол при вершине этих треугольников - общий.
Так как боковая сторона разделена на 3 равные части, то отношение сторон этих треугольников 1:2:3
Основание большего треугольника (его боковая сторона=боковая сторона трапеции) равно разности оснований:
5 - 2=3
Т.к. боковая сторона трапеции разделена на 3 равные части, отношение сторон меньшего ( верхнего) треугольника и большего равно 1:3
Следовательно, его основание равно
⅓ ·3=1 см
Отношение второго по величине треугольника и большего равно
2:3, отсюда его основание равно
⅖·3=2 см
Так как длина каждого из проведенных параллелльных отрезков больше оснований треугольников на 2, то:
длина искомых отрезков равна:
1 см+2=3 см
2см+2=4см
--------------------------------
2)
Стороны треугольника MNP относятся к сторонам АВС как 1:3,т.к. каждая сторона Δ АВС разделена в отношении 1:2. И эта одна часть - сторона Δ MNP, стороне же АВС остаются её 3 части.
Треугольники АВС и MNP подобны, так как их сходственные стороны пропорциональны и коэффициент подобия этих треугольников
k=1/3
Площади подобных фигур относятся, как квадрат их коэффициента подобия, а в этой задаче в отношении (1/3)²=1/9.
Площадь Δ MNP=1/9 площади тр-ка АВС и равна 1/9 от S или S/9
----------------
3)
Площади подобных фигур относятся, как квадрат их коэффициента подобия. Т.к. площади квадратов относятся как 25:9, то коэффициент подобия ( отношение сторон квадратов) равен
k=√(25/9)=5/3
Пусть сторона меньшего квадрата равна х.
Тогда сторона большего равна х+10
(х+10):х=5:3
По свойству пропорции
3(х+10)=5х
3х+30=5х
2х=30
х=15
Сторона меньшего квадрата равна 15
Проверка:
Площадь большего квадрата
(15+10)²=625
площадь меньшего
15²=225
625:225=25:9

АВ=ВС, АМ=МС
Док-ть: ВМ делит АС пополам
Р ABCM=26см, AB-CM=3см
АМ-?
1. Рассмотрим треугольники ABM и CBM. АВ=ВС, АМ=СМ по условию и ВМ-общая, значит треугольники равны.
2. Пусть H- точка пересечения ВМ с АС. Рассмотрим треугольники ABH и CBH. Т.к. АВС равнобедренный, то углы CAB и ACB равны, углы АВМ и СВМ равны по п.1, а AB=BC по условию, значит ABH=CBH AH=HС. Ч.т.д.
3. Рассмотрим ABCM. AB=BC, AM=CM. AB-CM=AB-AM=3. AB=3+AM
P=2×(AB+AM)
26=2×(3+AM+AM)
23=3+2AM
20=2AM
AM=10
ответ: АМ=10 см.