Всего бочек 21, значит каждому купцу в сумме должно достаться по 7 бочек
Теперь делим сам мёд:
Пусть половина бочки это одна доля. Тогда в полных бочках содержится 14 долей, а в полупустых 7 долей, всего 21 доля, из которых каждому купцу должно достаться по 7 долей. Исходя из этого, бочки следует распределить следующим образом:
1 купец: 3 полных бочки, 1 полупустая, 3 пустых. Всего бочек - 7, мёда - 3,5 бочки.
2 купец: 2 полных бочки, 3 полупустых, 2 пустых. Всего бочек - 7, мёда - 3,5 бочки.
3 купец: 2 полных бочки, 3 полупустых, 2 пустых. Всего бочек - 7, мёда - 3,5 бочки.
2√3 ед.
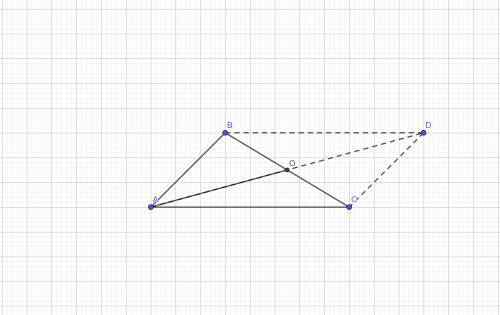
Объяснение:
Во условию в ΔABC AB=5 ед., AC=7 ед. , BC =10 ед.
Медиана АО - медиана, проведенная к большей стороне BC.
Достроим ΔABC до параллелограмма ABDC.
Диагонали параллелограмма пересекаясь, точкой пересечения делятся пополам , тогда AD= 2* AO.
По свойству квадратов диагоналей параллелограмма : сумма квадратов диагоналей параллелограмма равна сумме квадратов сторон.
AD² +BC² = 2*( AB²+AC²);
(2AO) ²+BC² = 2*( AB²+AC²);
4AO² +BC² = 2*( AB²+AC²);
4AO² + 10²=2*( 5²+7²);
4AO² = 2*( 25+49)-100;
4AO² =48;
AO² =48:4;
AO² =12;
AO= √12=√(4*3)=2√3 ед.
48=1\2*(5+х)*12
Думаю, ты его решишь.