такого треугольника не существует
или 60 см^2.
Объяснение:
Треугольника с заданными сторонами не существует.
13 см > 10см + 13мм, не выполнено неравенство для сторон треугольника.
Если в условии опечатка, длины стороны треугольника 13 см, 13 см, 10 см, то площадь может быть найдена по формуле Герона:
S = √p•(p-a)•(p-b)•(p-c).
p = (10+13+13):2 = 18 (см),
S = √18•(18-13)•(18-13)•(18-10) = √(18•5^2•8) = √(9•5^2•16) = 3•5•4 = 60 (см^2)
Ещё одним может быть нахождение по формуле
S = 1/2•a•h, где а = 10 см, а длина высоты найдена по теореме Пифагора из прямоугольного треугольника, образованного боковой стороной, высотой, проведённой к основанию, и половиной основания, h = 12 см.
(S = 1/2•10•12 = 60 (см^2) ).
Объяснение:
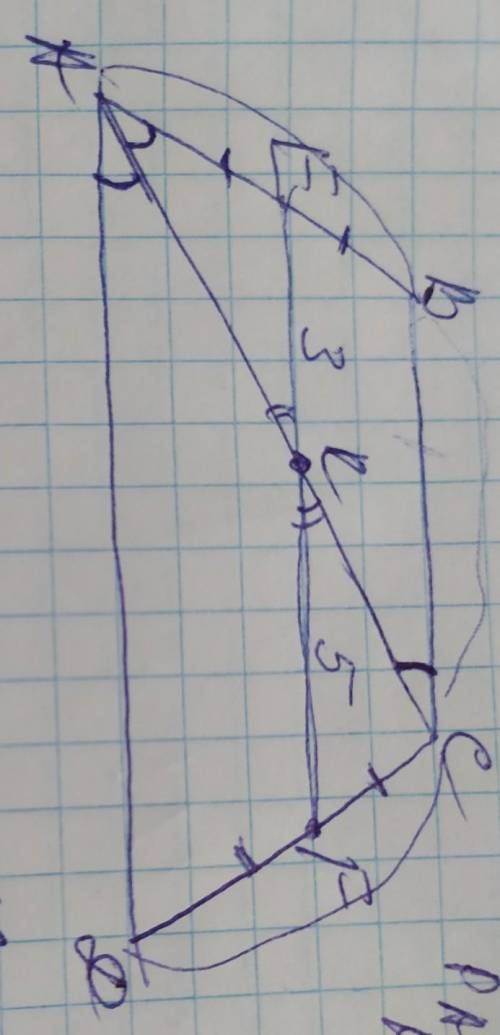
диагональ АС делит трапецию на 2 треугольника: АВС и АСД. Рассмотрим полученный ∆АСД. Так как точка Е - середина отрезка АВ, то точка F будет середина отрезка СД, следовательно EF является средней линией трапеции. Тогда KF будет являться средней линией ∆АСД (по теореме Фалеса: если прямая отсекает равные отрезки на одной стороне угла, то она отсекает равные отрезки и с другой стороны этого угла). По правилу треугольника его средняя линия=½ его основания, поэтому КF=½АД, или АД=2KF=5×2=10см
Если ЕF средняя линия трапеции, то она составит:
EK+KF=3+5=8см. Средняя линия трапеции вычисляется по формуле:
(ВС+АД)/2=EF. Используя эту формулу найдём сторону ВС:
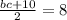
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
ВС+10=8×2
ВС+10=16
ВС=16–10=6см
Рассмотрим ∆АВС. В нём <ВАС=<САД, поскольку диагональ АС биссектриса угла А. Так как ВС||АД, то <САД=<ВСА как внутренние разносторонние поэтому <ВАС=<ВСА, следовательно ∆АВС равнобедренный и АВ=ВС. Поскольку трапеция равнобедренная, то АВ=СД=ВС=6см
Теперь найдём периметр трапеции зная её стороны:
Р=АВ+ВС+СД+АД=6×3+10=18+10=28см
ОТВЕТ: Р=28 см
а -длина второй стороны.
13*13(в квадрате) =5*5 + а * а, откуда
а=(извлечь корень квадратный из) =169-25=12см
Sпр=5 * 12=60см
Рпр=2 * (а + в) , где а, в -стороны прямоугольника,
Рпр=2 *(12см + 5см) = 34см