Две пересекающиеся прямые перпендикулярны, если они образуют четыре прямых угла
Геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки, является окружностью
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, является высотой треугольника
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
Две прямые на плоскости параллельны, если они не пересекаются
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны
Две прямые параллельны, если при пересечении их секущей соответственные углы равны
Если стороны одного угла являются продолжениями сторон другого, то углы вертикальные.
Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
(Все утверждения верны)
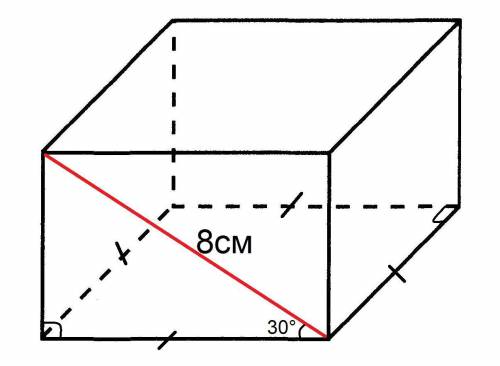
Рассмотрим один из двух треугольников, полученных при проведении диагонали в боковой грани параллелепипеда:
Треугольник прямоугольный т.к. параллелепипед прямой, по этой же причине один из острых углов равен 30°; гипотенуза (диагональ боковой грани) равна 8см; катет лежащий напротив угла в 30° (боковое ребро) равен половине гипотенузы: 8см:2 = 4см; другой катет (сторона основания), по теореме Пифагора, равен √(8²-4²) = √(64-16) = √48 см.
Объём параллелепипеда можно найти через его высоту (в нашем случаи это и боковое ребро) и площадь основания. В основании лежит квадрат, поэтому его площадь равна (√48 см)² = 48 см².
Тогда объём равен 4см · 48см² = 192 см³
ответ: 192см³.
Найдем 2ой катет, то есть расстояние
х=13^2-5^2=169-25=144=12^2
х=12