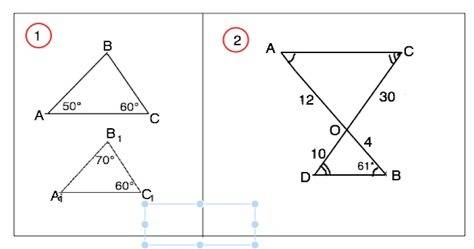
1) Сумма углов треугольника 180°. В ∆ АВС угол В=180°-50°-60°=70°. В ∆ А1В1С1 угол А1=180°-708-608=50°. Треугольники АВС и А1В1С1 подобны по равенству всех углов.
2) По условию АС║BD, АВ и СD - секущие. Образовавшиеся при пересечении секущими параллельных прямых накрестлежащие углы равны. ⇒ ∠СAО=∠DBO=61°. Треугольники АОС и BOD подобны по равенству накрестлежащих углов, а стороны, содержащие вертикальные углы при О - пропорциональны. k=АО:ВО=12:4=3, k=СО:DO=30:10=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. S(AOC):S(BOD)=k²=3²=9
№2. DABC – тетраэдр. М - середина АD. МК||(АВС). МК=3 см. Найдите длину ребра DC этого тетраэдра.
Тетраэдр — простейший многогранник, гранями которого являются четыре треугольника, т.е. треугольная пирамида. В условии не указаны длины ребер DABC. Поэтому решение даётся для правильного тетраэдра, все ребра которого равны.
МК||(АВС). МК лежит в плоскости ∆ АDC. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. ⇒ МК║АВ. Так как М – середина АD, а МК||АВ, то МК - средняя линия ∆ АDB и равна половине АВ ⇒ AD=АВ=2•МК=6 см.
* * *
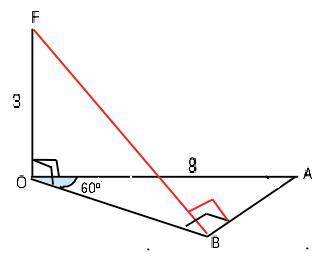
№3. ОАВ - прямоугольный треугольник (∠В=90°), ∠ АОВ=60°, АО=8 см, OF⊥АОВ). Найдите расстояние от точки D до прямой АВ, если OF=3 см.
Расстоянием от точки до прямой является длина отрезка, проведенного из данной точки перпендикулярно данной прямой. Треугольник АОВ прямоугольный, ОВ⊥ВА и является проекцией наклонной FB. По т. о 3-х перпендикулярах FB⊥АВ, поэтому является искомым расстоянием.
FО перпендикулярна плоскости ∆ АОВ. Если прямая, пересекающая плоскость, перпендикулярна этой плоскости, то она перпендикулярна каждой прямой, которая лежит в данной плоскости. ⇒ Треугольник FOB прямоугольный. FO=3 см (дано). ОВ=АО•cos60°=4см. В ∆ FOB по т.Пифагора FВ=√(FO²+OB²)=√(9+16)=5 см
5х + 5х + 2х = 96
12х = 96
х = 8
Значит, одна часть равна 8 см
Основание тогда равно 8см•2 = 16 см;
Боковые стороны равны 8 см• 5 = 40 см
ответ: 16 см; 40 см; 40 см.