Объяснение:
1)
Рисунок а.
Проведём две высоты ВМ и СК.
ВМ=АМ, так как ∆АВМ- прямоугольный, равнобедренный
cos45°=AM/AB
√2/2=AM/8
AM=8√2/2=4√2 см.
ВМ=4√2 см.
СК=ВМ=4√2 см.
∆СКD- прямоугольный треугольник.
СD- гипотенуза.
СК и KD- катеты
По теореме Пифагора найдем
КD²=CD²-CK²=6²-(4√2)²=36-32=4см
КD=√4=2 см.
МК=AD-AM-KD=16-4√2-2=14-4√2 см.
МК=ВС=14-4√2см.
S(ABCD)=BM*(BC+AD)/2=4√2(16+14-4√2)/2=
=2√2(30-4√2)=60√2-16 см².
ответ: 60√2-16см²
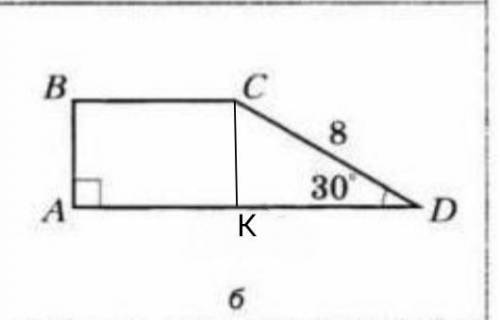
2) Рисунок б
Проведём высоту СК.
cos30°=KD/CD
√3/2=KD/8
KD=8√3/2=4√3 см
sin30°=CK/CD
1/2=CK/8
CK=8/2=4см высота трапеции.
BC=AD-KD=6√3-4√3=2√3 см.
S(ABCD)=CK(BC+AD)/2=4*(2√3+6√3)/2=
=2*8√3=16√3 см²
ответ: 16√3см²

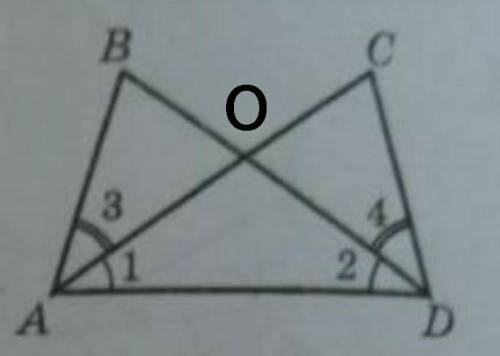
(примечание: "<" - угол)
Рассмотрим треугольники BAO и СОD:
<BAO=<CDA=b (по условию)
<BOA=<COD=а (как вертикальные)
<B=180°-<ВАО-<ВОА=180°-b-a
<С=180°-<СDA-<COD=180°-b-a =>
<B=<C=180°-b-a
ч.т.д.
(зачем тут равенство первого и второго угла я не очень понимаю, но предполагаю, что составители хотят немного другой , так что его я тоже могу сделать)
2:
Рассмотрим треугольник АОD:
так как <1=<2, то треугольник АОD - равнобедренный, следовательно, АО=ОD
Рассмотрим треугольники BAO и СОD:
<BAO=<CDA (по условию)
<BOA=<COD (как вертикальные)
АО=ОD (так как АОD - равнобедренный)
Следовательно, треугольники ВАО и СОD равны по 2-ому признаку, а значит, <В=<С
ч.т.д.
S=1/2*18*22
S=9*22=198
ответ: 198