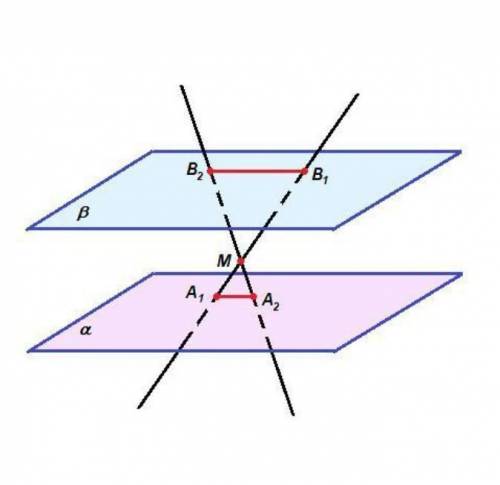
Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит
А₁А₂ ║ В₁В₂.
Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,
∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит
ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.
МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см
\dfrac{A_{1}A_{2}}{B_{1}B_{2}}=\dfrac{MA_{2}}{MB_{2}}
B
1
B
2
A
1
A2
=
MB
2
MA
2
Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,
\dfrac{x}{x+1}=\dfrac{4}{6}
x+1
x
=
6
4
6x = 4(x + 1)
6x = 4x + 4
2x = 4
x = 2
А₁А₂ = 2 см
По теореме косинусов cosA=(АВ²+АС²-ВС²)/(2АВ·АС)=(64+48-16)/(2·8·4√3)=√3/2 ⇒ ∠А=30°.
cosB=(АВ²+ВС²-АС²)/(2АВ·ВС)=(64+16-48)/(2·8·4)=1/2 ⇒ ∠В=60°.
∠С=180-∠А-∠В=180-30-60=90°.
В прямоугольном тр-ке, вписанном в окружность, гипотенуза является диаметром, значит радиус окружности равен её половине: R=АВ/2=8/2=4 см. - это ответ.