(x-5) ²+(y+9)²+(z+12)²=13² или (x-5) ²+(y+9)²+(z+12)²=169
Объяснение:
Перевод: Составить уравнение сферы с центром в точке (5; -9; -12), которая касается к оси ординат.
Решение.
Как известно, уравнение сферы имеет следующий вид:
(x-x₀) ²+(y-y₀)²+(z-z₀)²=R²,
где R - радиус сферы, (x₀; y₀; z₀) - координаты её центра.
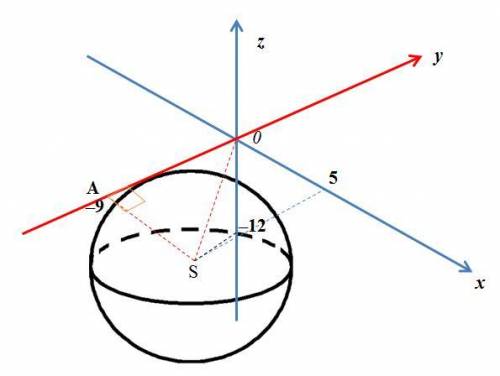
Нам известно координаты её центра S(5; -9; -12), остаётся найти радиус R (см. рисунок).
По условию сфера должна касаться к оси ординат и поэтому радиусом будет расстояние от центра S до оси Oy, то есть перпендикулярный к оси Oy отрезок, соединяющий центр S с точкой касания оси Oy (на рисунке нужная ось и нужные отрезки показаны красным).
Так как отрезок AS, равная радиусу R, перпендикулярен к оси Oy, то треугольник OAS прямоугольный. Тогда по теореме Пифагора
OS²=OA²+AS² или AS²=OS²-OA².
Длина отрезка OA известно: OA = |-9| = 9. Найдём OS² как квадрат расстояния между точками O(0; 0; 0) и S(5; -9; -12):
OS²=(5-0)²+(-9-0)²+(-12-0)²=5²+9²+12²=25+81+144=250.
Тогда
R²=AS²=OS²-OA²=250-9²=250-81=169=13² или
R=13.
Наконец, искомое уравнение сферы имеет вид:
(x-5) ²+(y+9)²+(z+12)²=13² или
(x-5) ²+(y+9)²+(z+12)²=169.
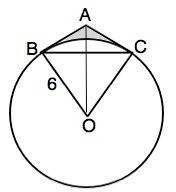
Вам известно уже, что угол C равен 90*, а это значит у вас ПРЯМОУГОЛЬНЫЙ треугольник
и потому вспомнить надо всего лишь Пифагора и что же такое синус этот и косинус ;)
Что такое КОСИНУС вам уже из дано даже подсказано cos A =7/25
т.е. косинус острого угла это отношение прилежащего катета к гипотенузе.
И потому вы уже имеете данные:
катет АС = 7; гипотенуза АВ = 25
теперь вспомним, что такое СИНУС этого угла А
Синус острого угла это отношение ПРОТИВОЛЕЖАЩЕГО катета к гипотенузе.
т.е. син А = ВС / АВ (1)
подставляем что нам известно
син А = ВС / 25
и видим, что надо найти катет ВС - как?
ну конечно тут Пифагор как всегда с^2 = a^2 + b^2
и в нашем случае это будет так:
AB^2 = AC^2 + BC^2 откуда =>
BC^2 = AB^2 - AC^2
или уже окончательно
BC = ( AB^2 - AC^2 )^(1/2)
находим
BC = ( 25^2 - 7^2 )^(1/2)
BC = ( 625 - 49 )^(1/2)
BC = ( 576 )^(1/2)
BC = 24
нашли!
теперь вернёмся к (1) со всеми данными получаем
син А = 24 / 25 ответ правильный геометрия 5
Искомую площадь можно найти по-разному.
1) Найти площадь четырехугольника АВОС и из нее вычесть площадь сектора круга.
2) Найти площадь ∆ АВС и из неё вычесть площадь сегмента. ограниченного дугой ВС и хордой ВС.
1) Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности⇒
∠ВАО=∠САО=120°:2=60°
∠АВО=∠АСО=90° т.к. радиусы, проведенные в точки касания, перпендикулярны касательным. ⇒
угол ВОС=60°, и ∆ ВОС - равносторонний.
∆ АВО=∆ АСО - прямоугольные.
АВ=BО:tg60°=6/√3=2√3
Длина дуги ВС =1/6 длины окружности, т.к. угол ВОС=1/6 полного круга.
◡ВС=2πr:6=12π:6=2π
P=AB+AC+◡BC=2•2√3+2π=4√3+2π = ≈13,2114 см
----------------
Ѕ (АВОС)=2Ѕ(АВО)=ВО•AB=6•2√3=12√3
S (сектора)=1/6πr²=36π:6=6π
S(фиг. АВС)=S(ABOC)-S(сект)=12√3-6π=6•(2√3-π)=≈1,935 см*
2) По второму попробуйте вычислить искомую площадь самостоятельно. Результат получится тот же, что найденная по первому
ответ: (x - 5)² + (y + 9)² + (z + 12)² = 169
Объяснение:
Для уравнения сферы нужен её радиус и центр.
В приложении представлено построение точки O (5; -9; -12). Красным выделен радиус сферы.
Обращаем внимание, что для поиска радиуса удобнее работать на модели справа -- прямоугольном параллелепипеде.
1. Радиусом будет расстояние от точки O до оси Y (так как необходимо кратчайшее расстояние до оси для касания сферы).
Расстояние от точки до прямой -- это перпендикуляр, проведённый из этой точки к данной прямой.
PN ⊥ NK, PN ⊥ NM (прямоугольный параллелепипед) ⇒ PN ⊥ (MNK) (по признаку ⊥ прямой и плоскости) ⇒ PN ⊥ NO (прямая, ⊥ плоскости, ⊥ любой прямой в этой плоскости) ⇒ NO -- искомый радиус.
2. MN = 5, MO = NK = 12. По теореме Пифагора из ΔNKO:
3. Уравнение сферы имеет следующий вид:
где R -- радиус сферы, (x₀, y₀, z₀) -- её центр.
Тогда в итоге получим следующее уравнение: