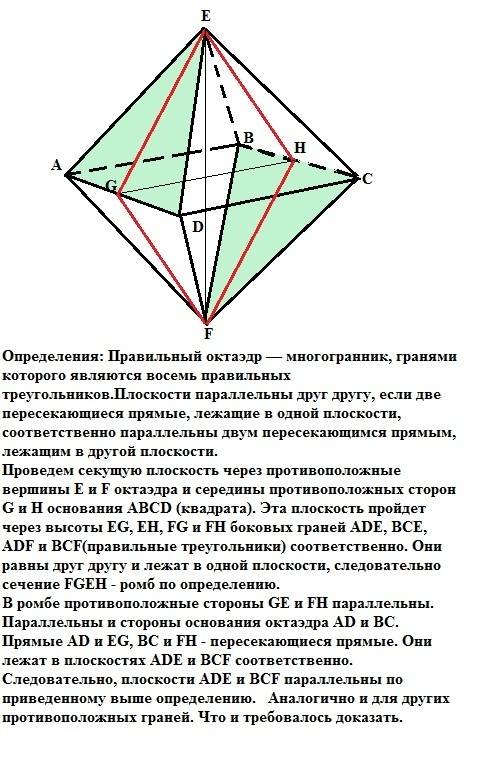
Определения: Правильный октаэдр — многогранник, гранями которого являются восемь правильных треугольников.
Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.
Проведем секущую плоскость через противоположные вершины Е и F октаэдра и середины противоположных сторон G и H основания АВСD (квадрата). Эта плоскость пройдет через высоты EG, EH, FG и FH боковых граней ADE, BCE, ADF и BCF(правильные треугольники) соответственно. Они равны друг другу и лежат в одной плоскости, следовательно сечение FGEH - ромб по определению.
В ромбе противоположные стороны GE и FH параллельны. Параллельны и стороны основания октаэдра AD и ВС. Прямые AD и EG, BC и FH - пересекающиеся прямые. Они лежат в плоскостях ADE и BCF соответственно. Следовательно, плоскости ADE и BCF параллельны по приведенному выше определению. Аналогично и для других противоположных граней. Что и требовалось доказать.
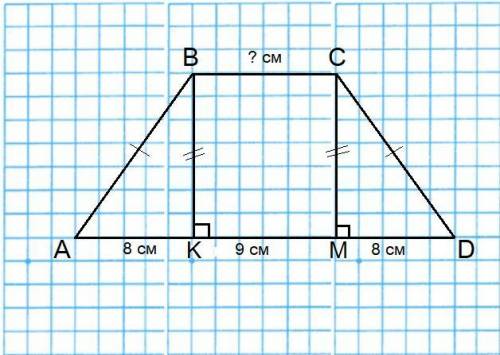
ответ: BC = 9 см.
Объяснение: Обозначим равнобедренную трапецию буквами ABCD. Тогда CM - высота, которая делит основание AD на указанные отрезки.
AB и CD - боковые стороны (между собой равные по свойству).
AD - большее основание, BC - меньшее основание.
Проведём из вершины B к большему основанию трапеции AD вторую высоту BK.
BK ⊥ AD; CM ⊥ AD ⇒ BK ║ CM ⇒ BK=CM (т.е. KBCM - прямоугольник).
Рассмотрим прямоугольные ΔABK и ΔMCD. Они равны (их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что трапеция ABCD - равнобедренная).
⇒ AK = MD = 8 см.
AD = AK + KM + MD = 25 см ⇒ KM = AD - (AK + MD) = 25 - 16 = 9 см.
Т.к. KBCM - прямоугольник ⇒ KM = BC = 9 см.
Тк угол равен 45(в прямоугольном треугольнике), то h=8 см