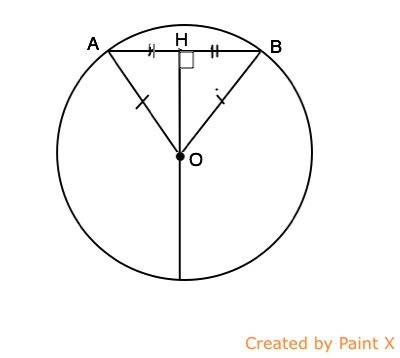
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
Т.к. данная сторона перпендикулярна диагонали, то получится два равных прямоугольных треугольника.
Найдём их площадь.
Как известно, площадь прямоугольного треугольника равна половине произведения его катетов.
Катетами являются соответственно диагональ и сторона, поэтому площадь параллелограмма равна S = 2•(1/2•17 см• 11 см) = 11•17см² = 187 см².
ответ: 187 см²/