1)
Радиус вписанной окружности правильного многоугольника совпадает с его апофемой (т.е. перпендикуляром, опущенным из центра на любую сторону)
Правильный шестиугольник можно разделить на 6 правильных треугольников. Его площадь равна площади 6 таких треугольников и S(шестиугольника)=6•S (треуг)
Нам известен радиус вписанной в шестиугольник окружности, т.е. высота правильного треугольника АОВ (см. рисунок). Для нахождения площади правильного треугольника воспользуемся формулой
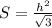
Тогда 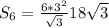 дм²
дм²
––––––––––
2)
По условию 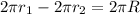
Примем коэффициент отношения радиусов окружностей равным а. Тогда радиус первой равен 5а, второй –3а
5a-3a=40⇒
a=20 см
r1=100 см=1м
S1=π•1²=π м²
60 см=0,6 м
S2=π•(0,6)²=0,36 м²
–––––––––––
3)
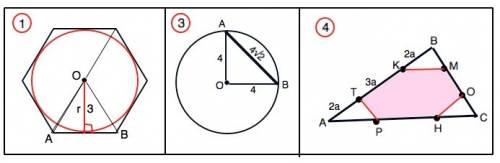
Найдите площадь сегмента круга, радиуса 4 см, если его хорда равна 4√2 см
Пусть центр круга О, хорда - АВ.
АО=ВО ⇒∆ АОВ - равнобедренный
По т.косинусов АВ²=АО²+ВО²- 2АО•ВО•cos∠AOB
32=2•16-2•16•cosAOB⇒
cos AOB=0, ⇒ ∠АОВ=90°.
Площадь искомого сегмента равна разности площадей сектора с углом 90° и прямоугольного ∆ АОВ.
Градусная мера полного круга 360°, значит, площадь сектора с углом 90°=1/4 площади круга
S сектора=16π:4=4π
S ∆ АОВ=4•4:2=4•2
S сегм=4π-4•2=4(π-2)= ≈4,566 см²
4)
Отношения отрезков сторон треугольника АВС, на которые их делят данные точки, одинаковы.
Примем коэффициент отношения отрезков сторон равным а.
Тогда АВ=7а.
Треугольники у вершин подобны треугольнику АВС, т.к. имеют общую вершину и стороны исходного треугольника пропорциональны сторонам треугольников, «отсекаемых» от него у вершин, с коэффициентом подобия 7:2, Поэтому эти отсекаемые треугольники равновелики.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
k=АВ:ВК=7:2 ⇒
S (ABC):S(BKM)=k²= 49/4
245:S(BKM)=49:4⇒
S(Δ BKM)=20
S(ТКМОНР)=245-3•20=185 мм²
h = 2•20 см²/4см = 10 см.
ответ: 10 см.