остроугольный и равнобедренный.
Объяснение:
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
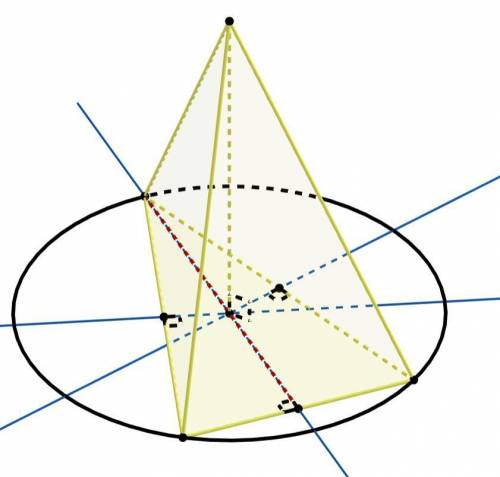
Объяснение:
4)
Сумма смежных углов равна 180°
Составляем уравнение.
7х+29+5х-5=180
12х+24=180
12х=180-24
12/х=156
х=156:12
х=13.
Первый угол равен 7х+29, подставляем значение х.
7*13+29=120°
Второй угол равен 5х-5, подставляем значение х.
5*13-5=65-5=60°
ответ; 120°;60°
5)
<АОD=180° развернутый угол.
<АОМ=<СОD, вертикальные углы.
<МОD=<AOD-<AOM=180°-28°=152°
ответ: <MOD=152°
6)
Пусть сторона АВ будет х, тогда сторона АС будет 2х, АС=СВ по условию. Составляем уравнение
х+2х+2х=20
5х=20
х=20/5
х=4 ед сторона АВ.
АС=СВ=2х, подставляем значение х.
2*4=8 сторона АС и СВ.
ответ: 4ед; 8ед; 8ед.