Условие не совсем корректное. В равностороннем треугольнике нет большей или меньшей стороны, на то он и равносторонний.
В сети можно найти несколько вариантов похожих задач с разными данными.
Вариант 1.
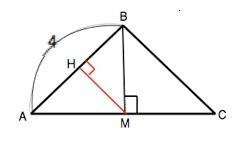
Решаем задачу о равнобедренном треугольнике АВС (АВ=ВС) с боковой стороной, равной 4, и большей стороной АС.
АС=0,75•(4+4)=6 см
Биссектриса угла против основания равнобедренного треугольника совпадает с высотой и медианой, поэтому АМ=СМ и ∆ АВМ=∆ СВМ – прямоугольные.
Искомое расстояние - высота МН треугольника АВМ.
cos BAM=AM:AB=3/4
MH=AM•sin HAM
sin(HAM)=√(1-cos*)=√(1- 9/16)=√7/4
MH=3√7/4
——
Возможно, задача все же о разностороннем треугольнике.
Вариант 2.
В разностороннем треугольнике большая сторона составляет 75% суммы двух других. Точка М, принадлежащая этой стороне, является концом биссектрисы треугольника. Найдите расстояние от точки М до меньшей стороны треугольника, если меньшая высота треугольника равна 4 см.
Здесь условие корректное - есть и большая сторона, и меньшая.
АС=0,75•(AB+BC)
По свойству биссектрисы треугольника ВМ делит противоположную углу сторону АС в отношении прилежащих сторон.
АВ:ВС=АМ:СМ
АМ=0,75 АВ
Меньшая высота - высота, проведена к большей стороне. ВК=4
Из формулы площади треугольника
ВК•AM=MH•AB
НМ=ВК•AM:AB ⇒ НМ=ВК•0,75 АВ:AB
HM=4•0,75=3 см
№8
ВСІІАD
KD-секущаяТреугольник КDC - равнобедренный
КС=DC
DC+KC+6=1/2P
DC+KC=48:2-6=18
DC=18:2=9(см)
№9
Верны Б и В
№10
(360-40*2):2=140 градусов - больший угол
№11
Сумма противолежащих углов четырехугольника,вписанного в окружность,равна 180градусов
112+97>180 градусов,значит,углы не противолежащие
180-97=83градуса - больший из оставшихся углов
№12
Треугольник АВС
АС - х
АВ - 5х
ВС^2=AB^2+AC^2
BC=корень из 5х*5х+х*х=корень из 26х^2
BC=5,1х
S=5х*х:2=18000
2,5х^2=18000
х=корень из 7200
х=84,85(м) - АС
Р=5х+5,1х+х=11,1х
Р=11,1*84,85=941,8(м) - периметр участка
№13 Подобие треугольников.
1,9:5=х:15
х=1,9:5*15
х=5,7(м) - фонарь висит на высоте 5,7м
№14
S=29*23=667
№15
Треугольник АВС
ВК-высота
АВ=ВС=(98-40):2=29(cм)
ВК^2=ВС^2-CK^2
ВК=корень из29*29-20*20
ВК=корень из 441
ВК=21
AK=40:2=20
S=20*21=420
1) уравнение стороны АС:
12х-9у+72 = 0, сократим на 3: 4х-3у+24 = 0 общий вид этого уравнения.
у = (4/3)х+8 уравнение с коэффициентом.
2) уравнение высоты, проведенной из вершины В.
Эта высота перпендикулярна АС и имеет коэффициент при х, равный -1/(4/3) = -3/4.
Уравнение высоты из точки В имеет вид у = (-3/4)х+в.
Для нахождения коэффициента в в полученное уравнение подставим координаты точки В.
1 = (-3/4)*1+в,
в = 1+(3/4) = 7/4.
Тогда уравнение примет вид у = (-3/4)х+(7/4) или в общем виде
3х+4у-7 = 0.
3) длина высоты из вершины В.
Надо найти координаты основания высоты как точку пересечения высоты и стороны АС.
4х-3у+24 = 0|x3 12x-9y+72 = 0
3х+4у-7 = 0|x-4 -12x-16y+28 = 0
______________
-25y+100 =0 y = 100/25 = 4.
x = (3y-24)/4 = (3*4-24)/4 = -12/4 = -3.
Точка Д(-3; 4). Длина высоты ВД равна:
BД = √((Хд-Хв)²+(Уд-Ув)²) = √25 = 5.
4) угол А. Для этого найдём длины сторон:
1) Расчет длин сторон
АВ = √((Хв-Ха)²+(Ув-Уа)²) = √50 = 7,071067812,
BC = √((Хc-Хв)²+(Ус-Ув)²) = √125 = 11,18033989,
AC = √((Хc-Хa)²+(Ус-Уa)²) = √225 = 15.
cos A= (АВ²+АС²-ВС²)/(2*АВ*АС) = 0,707107
A = 0,785398 радиан = 45 градусов.