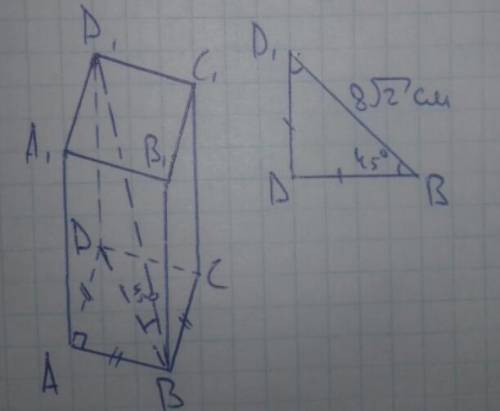
ABCDA₁B₁C₁D₁ - правильная четырёхугольная призма с основаниями ABCD и A₁B₁C₁D₁ .
Основания это квадраты т.к. призма прав., так же боковые рёбра перпендикулярны основаниям. Значит боковые грани это равные прямоугольники.
D₁B = 8√2 см.
В ΔD₁DB:
∠D₁DB = 90°; ∠D₁BD = 45° т.к. DB это проекция D₁B на основание ABCD; значит ∠DD₁B = 90°-45° = 45°.
ΔD₁DB - прямоугольный и равнобедренный с гипотенузой 8√2 см, поэтому катеты DD₁ и DB равны 8√2÷√2 = 8см.
В квадрате ABCD диагональ равна 8см, значит стороны равны 8÷√2 = 4√2 см.
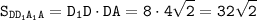см².
S(бок) = 4·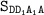 
= 4·32√2 = 128√2 см².
ответ: 128√2 см².
N7. Даны две линейные функции.Графиком функции является прямая.Чтобы понять пересекаются ли они -надо сравнить их угловые коэффициенты k ( это число которое умножается на Х ,стоит рядом с Х):
у =9 +х -здесь угловой коэффициент k= 1 (1x)
у =5х +6 - здесь угловой коэффициент k=5 (5х)
Угловые коэффициенты не равны( 1# 5),следовательно графики функций пересекаются.
Если бы угловые коэффициенты были равны ,то прямые были бы параллельны и не пересекались бы.Например:
у = 3х +2 - угловой коэффициент k1 =3 (3х)
у = 3х -10 - угловой коэффициент k2=3 (3х)
k1=k2- значит прямые графика функции параллельны.
б)3\4 - 2\5=15\20-8\20=7\20 или 0.35
в)2\5-1\4=8\20-5\20=3\20 или 0.15
г)1\4+1\5=5\20+4\20=8\20 или 0.4
ОТВЕТ: в) 0.15