
В равнобокой трапеции диагональ перпендикулярна боковой стороне и является биссектрисой острого угла при основании. Найти высоту трапеции , если ее площадь равна 9√3
Объяснение:
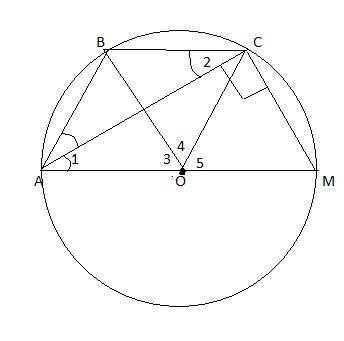
АВСМ-равнобедренная трапеция.
1)Если трапеция является равнобедренной, то около неё можно описать окружность. Пусть О-принадлежит АМ . Тогда ОА=ОС=ОМ как центры описанной окружности , т. к. центр описанной окружности лежит на середине гипотенузы .
2)Углы 1 и 2 равны как накрест лежащие при АМ||ВС, АС-секущая⇒ΔАВС-равнобедренный и ВА=ВС. Значит и ВА=ВС=МС.
3)ΔОАВ=ΔОВС=ΔОСМ по трем сторонам ВА=ВС=МС, остальные радиусы......Значит
- ∠3=∠4=∠5=180°:3=60°.
- их площади равны и S(ΔОСМ )=9√3:3=3√3.
3)В ΔОСМ ,∠СОМ=60° и ОС=ОМ ⇒ два других угла по 60°⇒этот треугольник равносторонний.
S( равност.тр)=(а²√3):4 .Найдем сторону треугольника (а²√3):4=3√3 или а²=12 , а=√12 .
Площадь можно найти иначе S( равност.тр)=1/2*а*h.
3√3=1/2*√12*h или h=3.
Объяснение:
т.к ДВ перпендикулярно и АВ и ВС, то следовательно АВ и ВС параллельны.
получается что АС секущая при параллельных прямых.
Соответственно угол ЕАВ= углу ЕСД (как внутренние накрест лежащие)
Угол АЕВ= углу СЕВ как вертикальные углы
рассмотрим 2 треугольника АВЕ и СДЕ
они равны по 2 признаку равенства прямоугольных треугольников
(если катет и прилежащий острый угол одного треугольника равен катету и прилежащему углу второго треугольника)
Катеты ДЕ и ВЕ равны по условию
Прилежащие острые углы также АЕВ=СЕД равны.
А если равны треугольники, то и их все стороны так же попарно равны.
Катет АВ= соответствующему катету ДС