В треугольнике, где угол 75°, второй равен половине прямого, то есть 45°, третий равен 180 - 75 - 45 = 60°.
Это один из острых углов прямоугольного треугольника.
Второй острый равен 90 - 60 = 30°.
Пусть катет против угла 30° градусов равен x, тогда катет против угла 60° равен x√3 (по тангенсу).
Площадь S = (1/2)x*x√3 = x^2*√3/2.
Приравняем её заданному значению.
x^2*√3/2 = 24*√3,
x^2 = 48,
x = √48 = 4√3. Это величина одного из катетов.
Второй равен 4√3*√3 = 12.
Гипотенуза равна √(4√3)^2 + 12^2) = √(48 + 144) = √192 = 8√3,
ответ: стороны равны 4√3, 12, 8√3.
24π см³ объем конуса
12π+8√3π см² площадь полной поверхности конуса.
Объяснение:
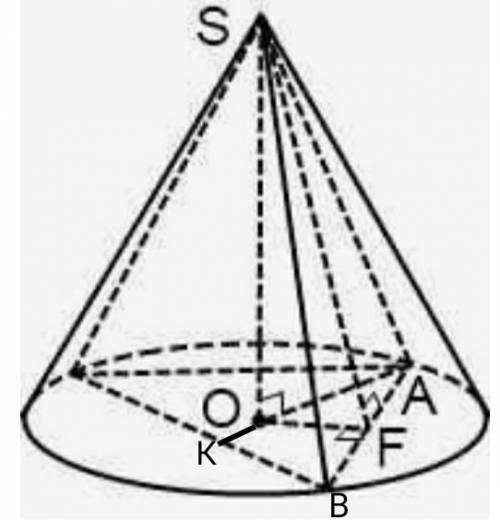
SA=4cм боковое ребро и образующая конуса
АВ=6 см сторона треугольника.
Треугольник равносторонний.
Из формулы нахождения высоты треугольника
AK=AB√3/2=6√3/2=3√3 см высота треугольника.
т.О делит высоту в отношении 2:1, начиная от вершины.
АО=3√3:3*2=2√3 см радиус конуса
∆SOA - прямоугольный.
SO и ОА- катеты
SA- гипотенуза.
По теореме Пифагора найдем высоту конуса
SO²=SA²-OA²=4²-(2√3)²=16-4*3=4см
SO=√4=2 см высота конуса
Формула нахождения объема конуса
V=πR²h/3
V=π*OA²*SO/3=π*(2√3)²*2=24π см³ объем конуса
Формула нахождения площади полной поверхности конуса
Sпол=πR(R+l)
Sпол=π*ОА(ОА+SA)=π*2√3(2√3+4)=
=12π+8√3π см² площадь полной поверхности конуса.
2) 2(a+b)=30
a+b=30/2=15
b=15-a
a (15-a)=56
15a-a*a=56
a*a-15a+56=0
D=225-224=1
a=(15+1)/2=8
b=15-8=7
ответ: а=8; b=7.