Объяснение:
ВС=АВ=11
∆ВDC: ∠D=90°
по теореме Пифагора:
ВD=√(BC²-CD²)=√(11²-5²)=√96=4√6
S(BDC)=1/2×CD×BD=1/2×5×4√6=10√6
S(BDC)=1/2×BC×DE
10√6=1/2×11×DE
20√6=11×DE
DE=20/11×√6
∆BЕD: ∠E=90°
по теореме Пифагора:
BE=√(BD²-DE²)=√((4√6)²-(20/11×√6)²)=
=√((16×6)-400×6/121)=√(96-2400/121)=
=√9216/121=96/11
S(BDE)=1/2×BE×DE=1/2×96/11×20/11×√6=
=960/121×√6
S(BDE)=1/2×BD×GE
960/121×√6=1/2×4√6×GE
960/121×√6=2√6×GE
960√6=242√6×GE
GE=960√6 / 242√6=960/242=480/121
EF=2×GE=2×480/121=960/121,т к ∆FBE -равнобедренный,высота ВG в равнобедренном треугольнике является медианой.
ответ: А) 960/121
Объяснение:
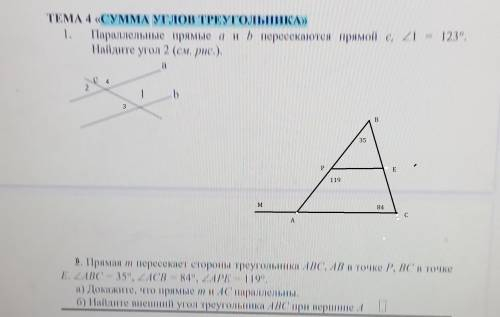
Углы 1 и 3, 2 и 4 - смежные, в сумме дают 180°.
Так как угол 1 равен 123°, то
∠3=∠2(как соответственные)=180°-123°=57°.
2) a) Сумма углов ΔАВС=180°.
∠A+∠B+∠C=180°. Следовательно,
∠А=180°-(∠В+∠С)=180°-(35°+84°)=180°-119°=61°.
Если m║AC, то угол ВРЕ равен углу ВАС.
Угол ВРЕ равен 180° - 119°=61°;
угол ВЕР=ВСА=180°-(61°+35°)=180°-96°=84°.
Следовательно, m║AC, что и требовалось доказать.
б) Теорема о внешнем угле треугольника:
Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом:
∠МАВ = ∠В+∠С=35°+84°=119°.
См. скриншот
В1D2=√249
Объяснение:
решение во вложении