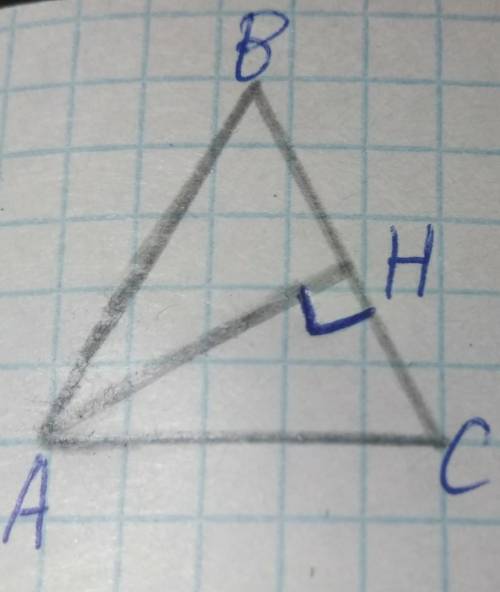
рисунок тут лёгкий, смотри. треугольник АВС- равнобедренный, нижнее основание AC=18 см, AB=BC- боковые стороны, угол ABC=120°, высота AH проведена из угла BAC к стороне BC. найти: AH.
Объяснение:
решение: 1) углы A+B+C=180°- по теореме о сумме углов треугольника, углы A+C=180-угол B=60°, углы А=С=30° как углы при основании равнобедренного треугольника
2)Треугольник AHC- прямоугольный так как АН- высота, угол АНС=90°, в прямоугольном треугольнике гипотенуза AC=18 см, а по свойству угла в 30°, катет AH, лежащий напротив гипотенузы, равен половине гипотенузы, то есть AH=9 см.
ответ: 9 см.
из условия ∠АОК=∠КОВ, ∠ВОМ=∠МОС и ∠КОМ=90°
∠КОМ=∠КОВ+∠ВОМ= 90°
т.к. ∠КОВ=∠АОК а ∠ВОМ=∠МОС значит ∠АОК+∠МОС= 90°
∠СОА= ∠СОМ+∠МОВ+∠ВОК+∠КОА= 90°+90°=180°
а значит он развернутый и значит точки С, О, А -лежат на одной прямой