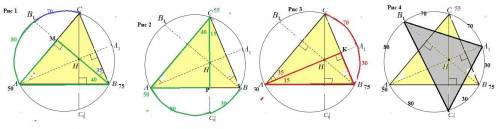
Ортоцентр H треугольника ABC отразили относительно сторон и получили точки A₁, B₁ и C₁. Найдите углы треугольника A′B′C′, если ∠A=50∘, ∠B=75∘.
Объяснение:
По свойству ортоцентра : "Точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной около него окружности". Значит все точки А, В, С,A₁, B₁ , C₁-лежат на окружности.
1)ΔАВМ -прямоугольный ,∠А=50°⇒ ∠АВМ=90°-50°=40° . Значит ∠МВС=75°-40°=35° .Поэтому дуги ∪ АВ₁=80° и ∪ В₁С=70° по т. о вписанном угле.
2)ΔАСР -прямоугольный ,∠А=50°⇒ ∠АСР=90°-50°=40° . Значит ∠РСВ=55°-40°=15° .Поэтому дуги ∪ АС₁=80° и ∪ С₁В=30° по т. о вписанном угле.
3)ΔАВК -прямоугольный ,∠В=75°⇒ ∠ВАК=90°-75°=15° . Значит ∠САК=50°-15°=35° .Поэтому дуги ∪ СА₁=70° и ∪ А₁В=30° по т. о вписанном угле.
)ΔА₁В₁С₁ , по т. о вписанном угле : ∠А₁=1/2*(80°+80)°=80° ,∠В₁=1/2*(30°+30)°=30° , ∠С₁=1/2*(70°+70)°=70°.
EO, OD, AO, OB, OC-радиус
DC, AB-диаметр
FC-хорда
2. 6см
Пояснение:
Чтобы ты понял:
Радиус-это отрезок, который начинается от центра окружности и заканчивается на окружности. Либо: отрезок, который соединяет центр окруж с окружностью
Диаметр-это отрезок, соед две точки окружности, проходящая через центр окружности. Иными словами, это как два равных радиуса, который вместе соединяются в центре, и получается как один длинный и развернутый отрезок.
Хорда-это отрезок, соед две точки окружности. То есть, она не проходит через центр, а просто соед две точки окруж.
Как я получил 6 см:
по усл, EO=3 см
EO явл радиусом окружности
АО-тоже радиус окружности.
Поэтому АО=ЕО (т.к центр окружности равноудалена от всех точек окружности, значит радиусы будут равны между собой)
=> АО=3см
AB-диаметр
Значит, AB=AO+OB
(т.к диаметр-это два равных между собой радиуса, соед в одну большой отрезок)
=>AO=OB
(по теор о радиусах равности(читай выше))
=> АО=ОВ=3 см
AB=АО+ОВ
АВ=3+3=6
∠1 = 180° -
∠2 =
ответ: 100°; 80°..