Определение: Параллелепипед — многогранник, у которого шесть граней и каждая из них — параллелограмм.
Требуется доказать, что противоположные грани параллелепипеда параллельны и равны.
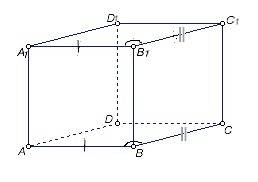
Докажем на примере оснований АВСD и A1B1C1D1 данного параллелепипеда.
Отрезки А1В1 и АВ параллельны и равны как стороны параллелограмма АА1В1В, отрезки В1С1 и ВС параллельны и равны как стороны параллелограмма ВСС1В1. ⇒
плоскости оснований параллельны по двум пересекающимся прямым.А1В1 и В1С1 одной плоскости и АВ и ВС противоположной.
Стороны параллелограммов АВСD и A1B1C1D1 равны , соответственные стороны углов А1B1C1 и ABC образованы параллельными прямыми,⇒ углы равны – эти параллелограммы равны, (их можно совместить наложением). Аналогично доказывается параллельность и равенство остальных граней. Доказано.
r=(a+b-c):2, где а и b – катеты, с - гипотенуза.
Медиана прямоугольного треугольника, проведенная к гипотенузе. равна её половине.
Следовательно, с=17•2=34 см
По т.Пифагора второй катет равен 30 ( отношение сторон этого треугольника из Пифагоровых троек 8:17:15, можно и не вычислять)⇒
r=(30+16-34):2=6 см