На стороне AB равностороннего треугольника ABC взята точка D так, что сумма расстояний от нее до сторон AC и BC равна 16 см. Найдите высоту треугольника, проведенную из вершины C.
РЕШЕНИЕ: Пусть сторона треугольника а. Одно из данных расстояний m, другое – n. Расстояния – это высоты. Находим площади треугольников:
Сюда относится картинка с умножением
Теперь их суммируем:
Сюда с сложением
В левой части полная площадь ABC, правую можно периписать так:
Сюда с сложением и умножением
Где h - высота из вершины C, равна сумме расстояний = 16 см
ОТВЕТ: 16 см
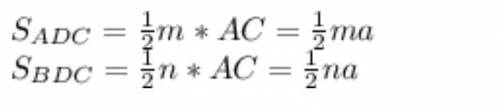
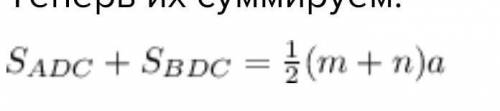
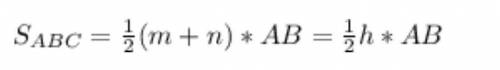
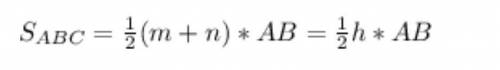
Точка пересечения серединных перпендикуляров треугольника является центром окружности, описанной около этого треугольника. Так как данный треугольник — равнобедренный, то по теореме о медиане равнобедренного треугольника медиана, биссектриса и высота треугольника, проведенные к основанию, совпадают. Значит, высота совпадает с серединным перпендикуляром, проведенным к основанию треугольника. Следовательно, центр окружности, описанной около равнобедренного треугольника, лежит на медиане, проведенной к основанию.
Объяснение:
ответ: 12 градусов