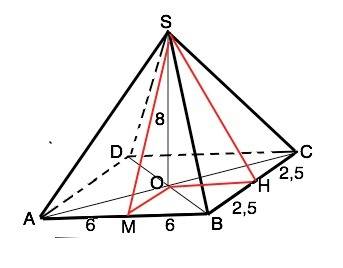
Основание пирамиды прямоугольник.
Его площадь 12•5=60 см²
Диагонали прямоугольника равны и в точке пересечения делятся пополам ⇒АО=ОВ=ОС=OD. Эти половинки диагоналей - проекции ребер пирамиды. Следовательно, ребра пирамиды как наклонные с равными проекциями равны. SA=SD=SC=SB
Боковые грани – 2 пары равных равнобедренных треугольников с основаниями 12 см и 15 см.
Высота SМ в ∆ASB=√(SO*+OM*)=√(64+6,25)=0,5√281
Высота SН в ∆BSC=√(SO²+OH²)=√(64+36)=10 см
S ∆ASB=AM•SM=6•0,5√281=3√281 см²
S ∆ BSC=BH•SH=2,5•10=25 см²
S бок=2•3√281+2•25=(6√281+50) см² или ≈150,58 см²
S полн=60+60√281+50=(110+60√281) см² или ≈210,58 см²
Основание пирамиды прямоугольник.
Его площадь 12•5=60 см²
Диагонали прямоугольника равны и в точке пересечения делятся пополам ⇒АО=ОВ=ОС=OD. Эти половинки диагоналей - проекции ребер пирамиды. Следовательно, ребра пирамиды как наклонные с равными проекциями равны. SA=SD=SC=SB
Боковые грани – 2 пары равных равнобедренных треугольников с основаниями 12 см и 15 см.
Высота SМ в ∆ASB=√(SO*+OM*)=√(64+6,25)=0,5√281
Высота SН в ∆BSC=√(SO²+OH²)=√(64+36)=10 см
S ∆ASB=AM•SM=6•0,5√281=3√281 см²
S ∆ BSC=BH•SH=2,5•10=25 см²
S бок=2•3√281+2•25=(6√281+50) см² или ≈150,58 см²
S полн=60+60√281+50=(110+60√281) см² или ≈210,58 см²

Противоположные стороны параллелограмма равны.
Продлим биссектрису AN до пересечения с прямой ВС.
∠1 = ∠2 так как AN биссектриса,
∠2 = ∠3 как накрест лежащие при пересечении параллельных прямых AD и ВС секущей AK, ⇒
∠1 = ∠3, ⇒ ΔАВК равнобедренный:
АВ = ВК = 9.
СК = ВК - ВС = 9 - 5 = 4
ΔAND подобен ΔКNC по двум углам (∠2 = ∠3 и углы при вершине N равны как вертикальные).
Обозначим NC - x, тогда DN - (9 - x),
Составим пропорцию:
AD : CK = DN : CN
5 : 4 = (9 - x) : x
5x = 36 - 4x
9x = 36
x = 4
CN = 4