Задача:
Длина окружности, вписанной в правильный треугольник, равна 12π см. Найдите периметр треугольника.
Чтобы найти периметр правильного Δ, нужно знать сторону; что найти сторону, нужно найти радиус вписанной окружности.
Дня нахождения радиуса окружности, воспользуемся формулой длины окружности и выразим из нее радиус:
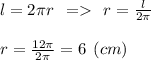
Теперь воспользуемся формулой радиуса вписанной окружности в правильный треугольник для нахождения стороны Δ:
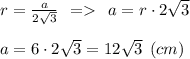
Осталось за малым — периметр правильного треугольника:
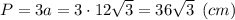
Периметр треугольника равен 36√3 см.
Углы в равностороннем треугольнике равны 60°. Биссектриса в таком треугольнике, проведенная из любой вершины, является высотой и медианой, деля его на 2 равных прямоугольных.
Рассмотрим один из прямоугольных треугольников:
∠α = 60/2 = 30° — по свойству биссектрисы. прилежащий к нему катет (h) — наша биссектриса. гипотенуза (c) — сторона треугольника.
Найдя гипотенузу прямоугольного треугольника, найдем и сторону равностороннего треугольника.
Воспользуемся формулой косинуса угла.
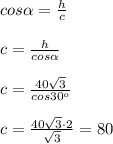
ответ: сторона равна 80.
Периметр прямоугольника находится по формуле:
P = 2(a + b)
По условию a/b = 2/3, отсюда 2b = 3a или же b = 1,5a.
Тогда P = 2(a + 1,5a) = 2,5•2a = 5a
40 = 2,5a
a = 16 см.
b = 3a/2 = 3•16/2 = 24 см.
Площадь прямоугольника S равна S = ab
S = 16 см•24 см = 384 см².