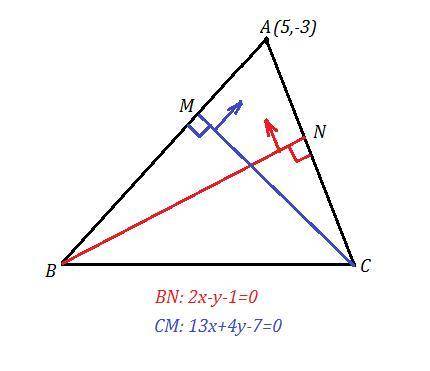
Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.
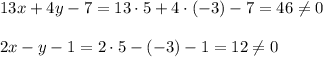
Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.
BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN:  .
.
Точка А(5,-3)∈АС и уравнение АС имеет вид:
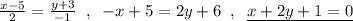
CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ:  .
.
Точка А(5,-3)∈АВ и уравнение АВ имеет вид:
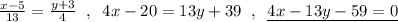
Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .
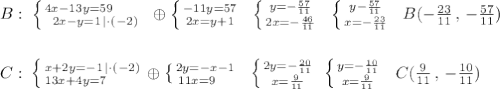
Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а) 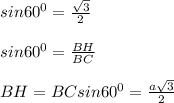
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
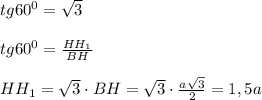
в) Найти площадь боковой поверхности - самая простая часть этого задания:
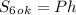 , где
, где 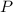 и
и  - периметр основания и высота пераллелепипеда соответственно.
- периметр основания и высота пераллелепипеда соответственно.

г) 
Отрезок АЕ = ВС = 36 см.
СЕ =√(АС²-АЕ²) = √(3600-1296) = √2304 = 48 см.
По свойству высоты СЕ из вершины прямого угла АСД:
ЕД/СЕ = СЕ/АЕ.
Отсюда ЕД = СЕ²/АЕ = 2304/36 = 64 см.
АД = 36 + 64 = 100 см.
2) ДС = 25 - 20 = 5 см.
Проверяем, подобны ли треугольники ABC и NDC?
ДС/ВС = 5/25 = 1/5.
CN/АС = 8/48 = 1/6. Нет - не подобны.