1) Катет 1= 4 корня из 3
катет 2= 4
2) 8 корней из 3
3) 4
Объяснение:
1) поскольку один угол 60 градусов, то второй 30, а мы знаем, что катет против угла в 30 градусов равен половине гипотенузы. Отсюда катет1 = 0.5*8=4. Так же мы знаем, что есть теорема пифагора.
8*8=(4*4)+(x*x)
64=16+x*x
x*x=48
x=корень 48
отсюда первый катет можно сократить как 4 корня из 3, второй катет равен 4
2)Площадь равна полупроизведению катетов, то есть (катет1*катет2)/2
(4*4корняиз3)/2, или (16корнейиз3)/2, или 8 корней из 3
3)Радиус описанной окружности - это половина ее диаметра, а диаметром описанной окружности вокруг прямоугольного треугольника - это его гипотенуза. Значит, радиус - это половина гипотенузы. 8:2=4
Объяснение:
Дано:
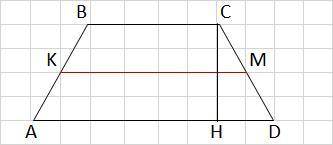
ABCD - трапеция
АВ = CD
ВС = 4
СН - высота
КМ = 10 (средняя линия: АК = КB, СМ = MD)
HD = ?
1) АВ = CD, т.е. трапеция - равнобедренная
2) Свойство трапеции: средняя линия трапеции параллельна основаниям и равна полусумме оснований:
КМ = (ВС + AD)/2
10 = (4 +AD)/2 → 20 = 4 + AD → AD = 20 -4 → AD = 16
3) Свойство равнобедренной трапеции:
Высота (CH), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AH), который равен полусумме оснований и меньший (HD), равный полуразности оснований:
HD = (AD - BC)/2 = (16 - 4)/2 = 6
HD = 6.
- треугольник АВС в основании пирамиды - прямоугольный с прямым углом В.
- SB - высота пирамиды H.
Площадь So основания равна:
So = (1/2)*6*3 = 9 см².
Объём V пирамиды равен:
V = (1/3)So*H = (1/3)*9*8 = 24 см³.