Добавлю "дурацкое алгебраическое" решение.
Пусть боковая сторона треугольника AB=BC=c, тогда AC =2c cos 40° (для упрощения писанины обозначение градуса буду опускать),
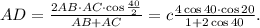
При этом 
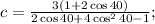

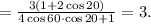
Мы воспользовались известными (как мне кажется) в школе формулами для длины биссектрисы через прилежащие стороны и угол, а также для длины отрезка стороны, на которую опущена биссектриса.
Возможно, приведет к успеху и другой путь - в этой задаче возникают углы в 60 (угол ADB) и 120 (соответственно угол ADC) градусов, поэтому можно написать хорошие тождества, скрепляющие элементы чертежа. При этом полезно провести биссектрису DF=BD угла ADC и достроить до ромба. Правда, с первого захода довести до ответе этот путь не удалось.

Я прощения за рисунок - там много лишнего, но можно разглядеть △ABC ∠AВC = 100°; у меня была очередная "сумасшедшая идея" :).
На самом деле порядок решения такой - берется ∠HAC = 20° и в него встраивается ломанная из звеньев одинаковой длины (пока не важно, какой). Это построение хорошо известно. Я его повторю только для тех, кто не в курсе (автор задачи, я уверен, прекрасно знает, я прощения).
Первая точка V на AC, вторая U на AH. △AUV равнобедренный => ∠UVC = 40°; следующая вершина ломаной точка F на AC, △FUV равнобедренный => ∠UFV = ∠UVC = 40° => ∠HUF = 60°; следующее звено FD, и легко увидеть, что △DUF оказался равносторонним. Еще одно звено DO, и точно также находится ∠DFO = ∠DOF = 80°; ∠FDO = 20°;
Так как ∠DAO = 20°, то ∠ADO = 80°; => △ADO равнобедренный, AD = AO;
Кроме того △ADO ∼ △FDO;
Больше нельзя добавить звеньев по прежней схеме, но можно добавить еще одно звено вдоль AC (сама точка C на русунке). Пусть CD продлено за D до точки B так, что AB = BC. Так как ∠DOС = 100°, ∠AСD = 40°; ∠ABС = 100°; AD - биссектриса ∠BAС.
То есть получился треугольник из условия задачи.
А вот теперь, собственно, решение задачи.
Так как ∠DFA = ∠DBA = 100°, точки F и B симметричны относительно биссектрисы AD, => DF = BD; => CO = BD; а так как AO = AD, то AD = AC - BD = 3; это все.
То, что звенья ломаной брались произвольной (одинаковой, но произвольной) длины, ничего не меняет - можно было сразу взять их длиной 3, например.
b=?
Высота трапеции равна диаметру окружности. h=2R=18.
Площадь трапеции S=h(a+b)/2 ⇒ (a+b)=2S/h=2·432/18=48.
B описанной трапеции h+с=a+b ⇒ с=a+b-c=48-18=30.
Опустим высоту на большее основание из тупого угла трапеции. Она разбивает это основание на два отрезка, один из которых равен меньшему основанию, а другой (х) образует прямоугольный треугольник вместе с наклонной боковой стороной и высотой.
х²=с²-h²=30²-18²=576,
x=24.
a=b+x=b+24.
a+b=48,
b+24+b=48,
2b=24,
b=12 - это ответ.