Дано:
тр АВС (уг С=90)
АС = 16 см
ВС = 12 см
АВ = 20 см
Найти:
а) косинус меньшего угла
б) сумму квадратов косинусов острых углов
а) по свойству соотношения сторон и углов треугольника, против меньшей стороны лежит меньший угол, а значит меньшим будет угол, лежащий против стороны 12 см, по условию, следовательно, это угол А.
cos A = AC / AB; cos A = 4/5 = 0.8
б) Есть св-во - оно же основное геометрическое тождество, сумма квадратов косинусов острых углов прямоугольного треугольника равна единице, но вы похоже этого ещё не изучали, посему надо найти оставшийся косинус угла В и найти сумму квадратов косинусов вычислением, приступим:
cos B = CB / AB; cos B = 12/20 = 3/5 = 0.6
cos²A +cos²B = 0.8²+0.6²=0.64+0.36=1
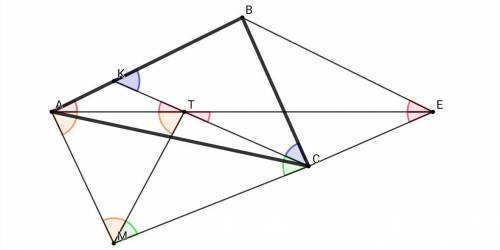
В ΔВСК (ВК = ВС) ∠ВКС = ∠ВСК = 40°. Отложим из точки В отрезок ВЕ, параллельный и равный КС ⇒ КВЕС - параллелограмм, КС = ВЕ = АВ, ΔАВЕ - равнобедренный, ∠АВЕ = 140° ⇒ ∠ВАЕ = ∠ВЕА = 20° ⇒ ∠ВЕА = ∠СЕА = 20° ⇒ ΔTCE, ΔAKT - равнобедренные, TC = CE = a, AK = KT = b. Отложим на продолжение СЕ отрезок ТМ, равный ТС ⇒ ∠TCM = ∠TMC = 40°, ∠CTM = 100°, ∠ATM = 160° - 100° = 60°. В ΔАТМ (AT = TM) ∠ATM = 60° ⇒ ΔATM - правильный, АT = TM = AM = TC = a. В ΔATC (AT = TC) ∠TAC = ∠TCA = 10° ⇒ ∠BAC = 20° + 10° = 30° и можно заметить, что ВАМС - параллелограмм.